The Basics Of Transformers
This document explains the basic theory and operation of transformers
UPDATED AUG 29 2024
1. Introduction to Transformers
Transformers are essential components of electrical and electronic systems.
Providing electrical isolation and carrying out the vital task of transforming voltages and current. Even though the design process can sometimes be viewed as an “art” , their construction and functionality are based on fundamental physics principles.
This article delves into the basics of transformer theory, operation, and performance, offering insights into their core characteristics and practical considerations.
2. Basic Transformer Theory
Transformers provide electrical isolation between circuits, which is crucial for safety and functionality in different applications.
A transformer consists of a magnetic core with primary and secondary coils wound around it.
When an alternating voltage is applied to the primary coil, it will generate an alternating current that corresponds to alternating magnetic flux in the core.
This flux induces a voltage in both secondary and primary coil thus; Faraday’s Law of Induction in action.
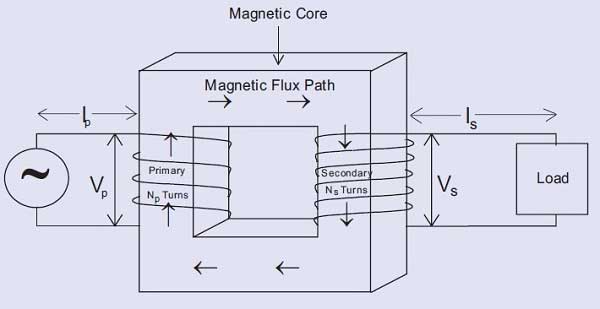
The above figure represents the essential elements for a transformer: a magnetic core with a primary and secondary coil wound on the limbs of the magnetic core.
An alternating voltage (Vp) applied to the primary creates an alternating current (Ip) through the primary.
This current produces an alternating magnetic flux in the magnetic core.
This alternating magnetic flux induces a voltage in each turn of the primary and in each turn of the secondary.
As the flux is a constant, i.e. the same in both primary and secondary:
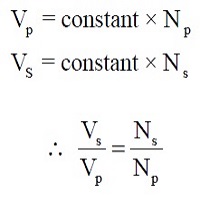
This equation shows that a transformer can be used to step up or step down an ac voltage by controlling the ratio of primary to secondary turns. (Voltage transformer action).
It can also be shown that:
Primary Volt Amperes = Secondary Volt Amperes
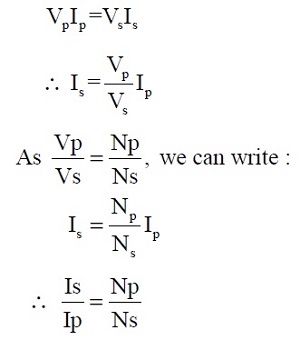
This equation shows that a transformer can be used to step up or step down an ac current by controlling the ratio of primary to secondary turns.
(Current transformer action)
It will be noted that there is no electrical connection between the primary and secondary windings.
A transformer, therefore, provides a means of isolating one electrical circuit from another.
These features - voltage/current transformation and isolation - cannot be obtained efficiently by any other means, with the result that transformers are used in almost every piece of electrical and electronic equipment in the world.
3. B-H curves
Magnetic properties of the core material greatly influence the performance of a transformer. When the transformer’s primary coil is energized, the magnetizing current creates a magnetizing force (H), which generates magnetic flux (B) in the core. This relationship between the B and H is represented by the B-H curve of the material.
The magnetizing force (H) is equal to the product of magnetizing current and the number of turns, and is expressed as Ampere - Turns.
B-H curves illustrate the flux density as the function of the magnetizing force, it means that as the (H) Increases, (B) rises until the core material is saturated.
At saturation, further increases in (H) do not significantly increase (B) and the reason why designing transformers to operate below the saturation point is crucial to ensure efficient performance.
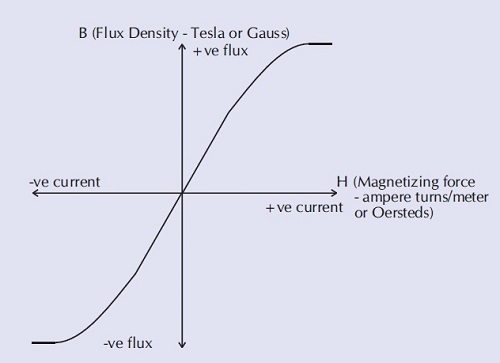
From the B-H curve it can be seen that, as the magnetizing force is increased from zero, the flux increases up to a certain maximum value of flux.
Above this level, further increases in magnetizing force result in no significant increase in flux. The magnetic material is said to be 'saturated'.
A transformer is normally designed to ensure that the magnetic flux density is below the level that would cause saturation.
The flux density can be determined using the following equation:
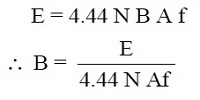
Where:
E represents the RMS value of the applied voltage.
N represents the number of turns of the winding.
B represents the maximum value of the magnetic flux density in the core (Tesla).
A represents the cross-sectional area of the magnetic material in the core (sq. meters).
f represents the frequency of the applied volts.
Note
1 Tesla = 1 Weber/meter²
1 Weber/m² = 10,000 Gauss
1 Ampere-turn per meter = 4 p x 10-3 Oersteds
In practice, all magnetic materials, once magnetized, retain some of their magnetisation even when the magnetizing force is reduced to zero.
This effect is known as 'remanence' and results in the B-H curve for the material exhibiting a response to a decreasing magnetizing force that is different to the response to an increasing magnetizing force.
In practice real magnetic materials have a B-H curve as follows:
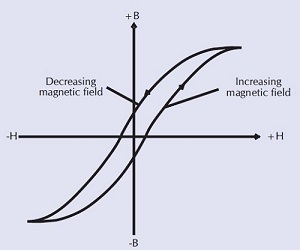
The curve shown above is termed the 'hysteresis' loop of the material, and it represents the true B-H response of the material. (The first B-H curve represented the average or mean of the true B-H loop response).
The slope of the B-H curve, the saturation level, and the size of the hysteresis loop are dependent on the type of material used, and on other factors.
This is illustrated using the following examples:
 |
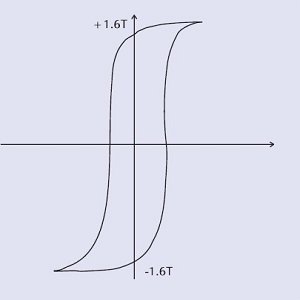Low-grade iron core High-saturation flux density Large loop = large hysteresis loss Suitable for 50/60Hz |
 |
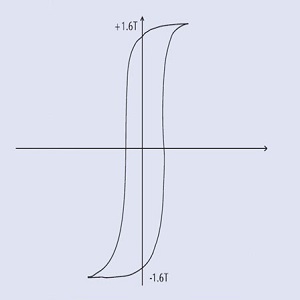High-grade iron core High-saturation flux density Medium loop = medium hysteresis loss Suitable for 400 Hz transformers |
 |
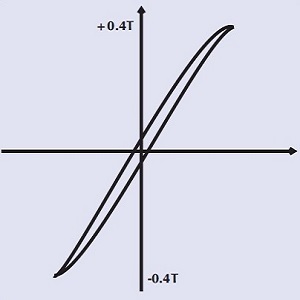Ferrite core - no air gap Medium-saturation flux density Small loop = small hysteresis loss Suitable for-high frequency transformers |
 |
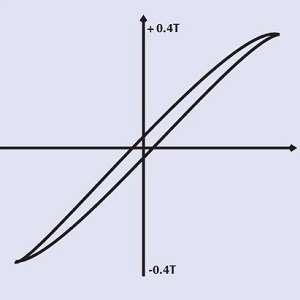Ferrite core - large air gap Small loop = small hysteresis loss Suitable for high-frequency Inductors with large DC current |
4. Hysteresis Loss
The B-H curve exhibits a phenomenon called hysteresis.
This is a phenomenon where the magnetization of the core material lags behind the magnetizing force – the energy losses resulting from this event is known as the hysteresis loss.
Materials with larger hysteresis loops incur higher losses.
This loss is represented by the area enclosed within the B-H hysteresis loop.
Therefore, transformer cores are designed with materials that have low hysteresis loss to enhance efficiency.
5. Eddy Current Loss
Eddy currents (also called Foucault's current) are loops of electrical current induced within the core material by the alternating magnetic flux.
The currents create resistive loss which leads to heating of the core known as Eddy Current Loss as they look like eddies or whirlpools.
To minimize the losses, transformer cores are made from laminated sheets or ferrite materials, which restrict the paths for these currents.
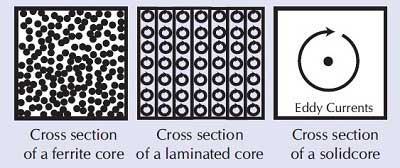
6. Transformer Equivalent Circuit
An ideal transformer with one primary winding and two secondary windings can be represented as shown below
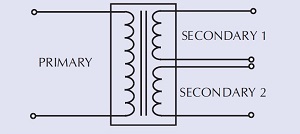
Such a transformer has the following characteristics:
-
- No losses
- Perfect coupling between all windings
- Infinite open circuit impedance (i.e., no input current when secondaries are open-circuited).
- Infinite insulation between windings
In practice, transformers differ from the ideal model due to various non-ideal characteristics. The transformer equivalent circuits incorporate these aspects:
-
- Winding Resistances
- Capacitances
- Core Losses
- Magnetizing Inductance
- Leakage Inductances
These variables aid in forecasting transformer performance and deviations from the ideal model.
Many of these characteristics can be represented by a transformer equivalent circuit:
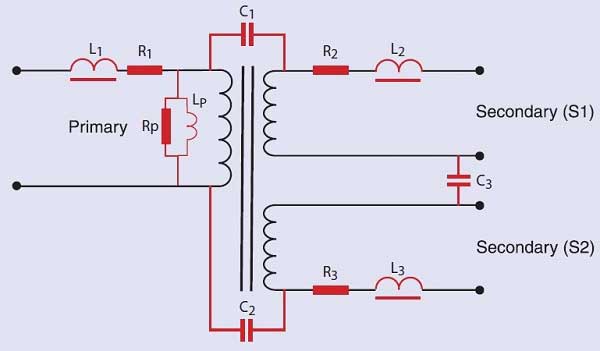
Where:
R1, R2, R3 represent the resistance of the winding wire.
C1, C2, C3 represent the capacitance between the windings.
Rp represents the losses which are due to the eddy current and hysteresis losses. These are the real power losses, sometimes called the core loss, that may be measured by performing an open-circuit power measurement. Because there is no load current, there is very little I2R copper loss in the energized winding, and the watts measured at no load are nearly all due to the core.
Lp represents the impedance due to the magnetizing current. This is the current that generates the magnetizing force, H, used in the B-H loop diagrams. Note that this current may not be a simple sine wave, but can have a distorted, peaked shape, if the transformer is operated in the non-linear region of the B-H curve. This is usually the case for line-frequency, laminate type transformers.
L1, L2, L3 represent the leakage inductance of each of the windings. (This is discussed in detail in Voltech Note 104-105, "Leakage Inductance".)
7. Conclusions
The equivalent circuit of a transformer reflects the real properties of the magnetic circuit comprising the core and windings.
The equivalent circuit can therefore be used with confidence to understand and predict the transformer's electrical performance in a variety of situations.
Grasping the basic principles and practical considerations of transformer operation equips engineers to design, test, and apply transformers effectively across diverse applications.
8. Further Reading
Understanding the equivalent circuit of a transformer enables engineers to analyze and predict its electrical performance in various operational conditions. It also aids in optimizing design and testing processes, ensuring transformers meet quality and efficiency standards.
Further technical notes in this series discuss how the equivalent circuit parameters are used to derive practical tests for transformers to guarantee their quality in a manufacturing environment.