AC-Theorie
In den heutigen fortschrittlichen Wechselstromanwendungen sind Verbesserungen bei der Messung und dem Verständnis komplexer Strom- und Spannungsverhältnisse immer wichtiger geworden.
Dieser Leitfaden bietet einen Überblick über die grundlegenden Parameter der AC-Theorie und ihre Bedeutung.
Durch das Erlernen der grundlegenden Konzepte von Effektivwerten, Durchschnittswerten, Wirk- und Scheinleistung, Leistungsfaktor, Scheitelfaktor, harmonischer Verzerrung und Messtechniken können Sie die fundamentale AC-Theorie besser verstehen.
AKTUALISIERT 29. AUGUST 2024
1. RMS (quadratischer Mittelwert)
Der Effektivwert ist das am häufigsten verwendete und nützlichste Mittel zur Angabe des Werts von Wechselspannung und -strom.
Der Effektivwert einer Wechselstromwellenform ist der Wert, der bei Anwendung auf einen gegebenen Stromkreis für eine gegebene Zeit den gleichen Energieaufwand erzeugt, wenn eine Gleichstromquelle für den gleichen Zeitraum auf den gleichen Stromkreis angewendet wird.
Der Effektivwert ist wichtig für die Bewertung der von einer Wechselstromquelle verfügbaren Leistung und ein wichtiges Maß für die Quantifizierung von Wechselspannung und -strom.
BERECHNUNG:
Die Berechnung eines Effektivwerts lässt sich am besten anhand einer Wechselstromwellenform und der damit verbundenen Erwärmungswirkung beschreiben, wie sie in Abb. 1(a) unten dargestellt ist:
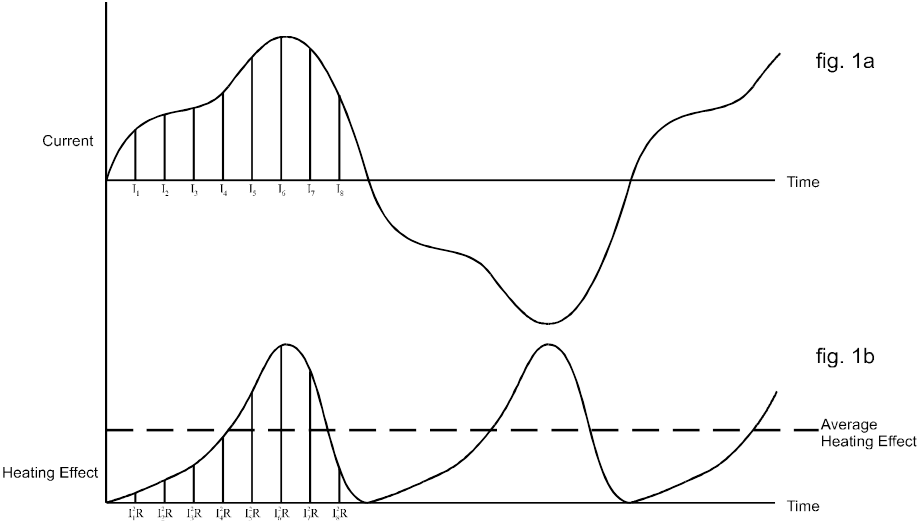
Wenn man davon ausgeht, dass dieser Strom durch einen Widerstand fließt, ergibt sich die Heizwirkung zu jedem Zeitpunkt aus der folgenden Gleichung:
![]()
Durch Aufteilen des Stromzyklus in gleichmäßig verteilte Koordinaten kann die zeitliche Variation des Heizeffekts bestimmt werden, wie in Abb. 1b dargestellt.
Die durchschnittliche Heizleistung (Leistung) ergibt sich aus:
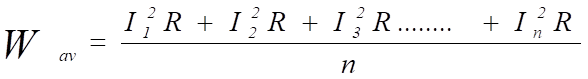
Wenn wir den entsprechenden Stromwert ermitteln möchten, der den oben gezeigten durchschnittlichen Heizeffektwert erzeugen würde, dann gilt das Folgende:
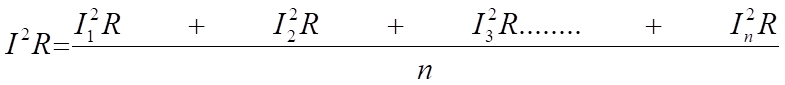
daher
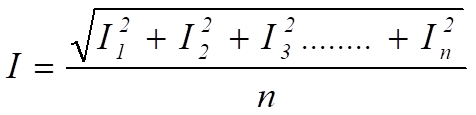
= die Quadratwurzel des Mittelwertes der Quadrate des aktuellen
= der Effektivwert des Stroms .
Dieser Wert wird oft als Effektivwert der Wechselstromwellenform bezeichnet, da er dem Gleichstrom entspricht, der in der ohmschen Last dieselbe Heizwirkung (Leistung) erzeugt.
Für eine reine Sinuswellenform:
RMS = Spitzenwert / SQRT (2)
= Spitzenwert x 0,707
2. Durchschnittswert
Der Durchschnittswert einer Sinuswelle ist der Mittelwert aller Momentanwerte eines halben Zyklus, da der Durchschnittswert über einen vollen Zyklus bei symmetrischen Wellenformen wie der AC-Wellenform Null ist.
Der Durchschnittswert einer Wellenform wie in Abb. 2 dargestellt ergibt sich aus:
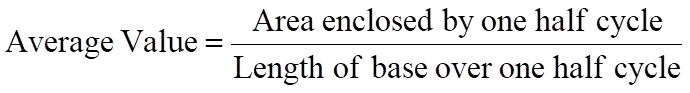
Es ist klar, dass der Durchschnittswert nur über einen halben Zyklus der Wellenform eine echte Bedeutung haben kann, da bei einer symmetrischen Wellenform der Mittel- oder Durchschnittswert über einen vollständigen Zyklus Null ist.
Die meisten einfachen Multimeter ermitteln Wechselstromwerte durch Vollweggleichrichtung der Wechselstromwellenform, gefolgt von einer Berechnung des Mittelwerts.
Solche Messgeräte werden jedoch in RMS kalibriert und nutzen die bekannte Beziehung zwischen RMS und Durchschnitt für eine sinusförmige Wellenform.
zB: RMS = 1,11 x Mittelwert.
Bei anderen Wellenformen als einer reinen Sinuswelle sind die Messwerte solcher Messgeräte jedoch ungültig.
3. Wirk- und Scheinleistung (W & VA)
Die Wirkleistung ist die tatsächliche Menge an Leistung, die in einem Stromkreis verbraucht oder verbraucht wird, während die Scheinleistung die Kombination aus Wirkleistung und Blindleistung ist.
Es handelt sich um das Produkt aus Spannung und Strom eines Stromkreises ohne Bezug zum Phasenwinkel.
Da die Scheinleistung in direktem Zusammenhang mit dem Effektivwert steht (beide wurden als tatsächliche Menge und Effektivwert von Wechselstrom und Wechselspannung definiert), lautet die einfache Formel für die Scheinleistung S (Scheinleistung) = V(Effektivwert) x I (Effektivwert) und wird in Voltampere (VA) gemessen.
ANWENDUNG:
Wenn eine sinusförmige Spannungsquelle von beispielsweise 100 V RMS an eine ohmsche Last von beispielsweise 100 Ohm angeschlossen wird, können Spannung und Strom wie in Abb. 3a dargestellt werden und gelten als in Phase.
Die Leistung, die zu einem beliebigen Zeitpunkt von der Versorgung zur Last fließt, ergibt sich aus dem Produktwert aus Spannung und Stromstärke zu diesem Zeitpunkt, wie in Abb. 3b dargestellt.
Daraus ist ersichtlich, dass die in die Last fließende Leistung (bei der doppelten Versorgungsfrequenz) zwischen 0 und 200 Watt schwankt und dass die an die Last abgegebene Durchschnittsleistung 100 Watt beträgt – was man bei 100 V RMS und einem Widerstand von 100 Ohm auch erwarten würde.

Wenn die Last jedoch reaktiv ist (d. h. sowohl Induktivität oder Kapazität als auch Widerstand enthält) und eine Impedanz von 100 Ohm hat, beträgt der fließende Strom zwar immer noch 1 A RMS, ist aber nicht mehr in Phase mit der Spannung. Dies ist in Abb. 4a für eine induktive Last mit einem um 60 ° nacheilenden Strom dargestellt.
Obwohl der Leistungsfluss weiterhin mit der doppelten Netzfrequenz schwankt, fließt er jetzt nur während eines Teils jeder Halbwelle von der Versorgung zur Last – während des verbleibenden Teils fließt er tatsächlich von der Last zur Versorgung.
Der durchschnittliche Nettostromfluss in die Last ist daher viel geringer als im Fall einer ohmschen Last, wobei an die induktive Last nur 50 W Nutzleistung abgegeben werden.
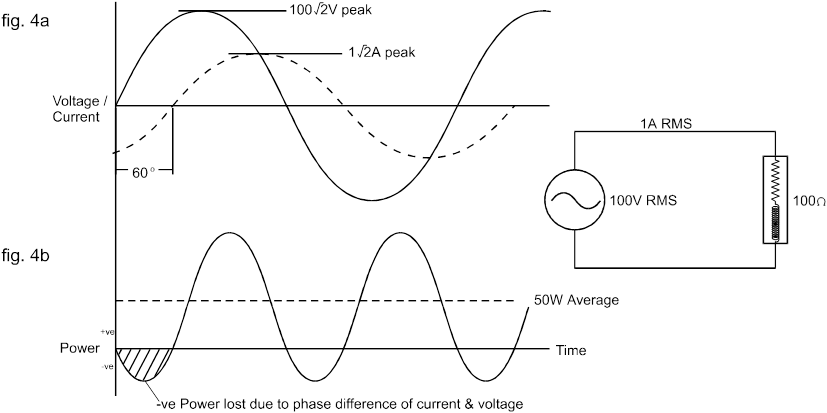
In beiden oben genannten Fällen betrug die Effektivspannung 100 V RMS und der Strom 1 A RMS.
Das Produkt dieser beiden Werte ist die an die Last abgegebene Scheinleistung und wird in VA wie folgt gemessen:
Scheinleistung = Volt RMS x Ampere RMS
Um die Wirkleistung zu ermitteln, reicht die bloße Kenntnis der Effektivspannung und des Effektivstroms nicht aus.
Um die Leistung genau zu messen – etwa um Wärmeverlust oder Effizienz auszuwerten – benötigen wir ein echtes Wechselstrom-Leistungsmessgerät.
Dieses Gerät berechnet das Produkt aus momentanen Spannungs- und Stromwerten und zeigt dann den Durchschnitt dieses Produkts an.
4. Leistungsfaktor
Es ist klar, dass im Vergleich zu Gleichstromsystemen die übertragene Wechselstromleistung nicht einfach das Produkt der Spannungs- und Stromwerte ist.
Der Leistungsfaktor ist definiert als das Verhältnis von Wirkleistung zu Scheinleistung.

Bei rein sinusförmigen Wellenformen von Wechselstrom und -spannung hängt der Leistungsfaktor von der Phase des Winkels ab, in dem er gemessen wird.
Der Leistungsfaktor beträgt Eins (1), wenn Spannung und Strom in der gleichen Phase sind. (und Cos (0) = 1)
Beim nacheilenden Leistungsfaktor hinkt der Strom der Spannung um einen spitzen Winkel hinterher.
Beim voreilenden Leistungsfaktor eilt der Strom der Spannung um einen spitzen Winkel voraus.
Der Leistungsfaktor beträgt Null, wenn Spannung und Strom genau um 90 Grad phasenverschoben sind. Dies bedeutet, dass auch die WIRKLICHE Leistung Null beträgt.
Bedeutung: Der Leistungsfaktor beeinflusst die Energieeffizienz und Lasthandhabung in Wechselstromsystemen.
BERECHNUNG:
Im vorherigen Beispiel (Wirk- und Scheinleistung) mit induktiver Last beträgt der Leistungsfaktor 0,5, da die Nutzleistung genau die Hälfte der Scheinleistung beträgt.
Bei sinusförmigen Spannungs- und Stromwellenformen ist der Leistungsfaktor tatsächlich gleich dem Kosinus des Phasenwinkels zwischen den Spannungs- und Stromwellenformen.
Beispielsweise hinkt bei der zuvor beschriebenen induktiven Last der Strom der Spannung um 60 ° hinterher. Daher gilt:
![]()
Aus diesem Grund wird der Leistungsfaktor häufig als cosθ bezeichnet.
Es ist jedoch wichtig zu beachten, dass dies nur der Fall ist, wenn sowohl Spannung als auch Strom sinusförmig sind (Abbildung 5, I1 und I2) und dass der Leistungsfaktor in allen anderen Fällen nicht gleich cosθ ist [Abbildung 5 (I3)].
Dies muss bei der Verwendung eines Leistungsfaktormessgeräts beachtet werden, das cosθ anzeigt, da der Messwert nur bei rein sinusförmigen Spannungs- und Stromwellenformen gültig ist.
Ein echtes Leistungsfaktormessgerät berechnet das Verhältnis von Wirk- zu Scheinleistung wie oben beschrieben.
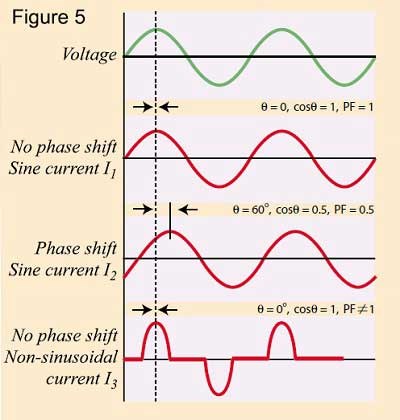
5. Scheitelfaktor
Es wurde bereits gezeigt, dass für eine sinusförmige Wellenform gilt:
![]()
Das Verhältnis zwischen Spitze und Effektivwert wird als Crest-Faktor bezeichnet und ist definiert als das Verhältnis von Spitzenwert und Effektivwert (RMS).
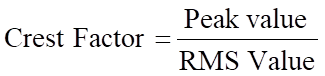
Für eine Sinuskurve gilt also:
![]()
Viele moderne, an die Wechselstromversorgung angeschlossene Geräte weisen nicht sinusförmige Stromwellenformen auf. Dazu zählen beispielsweise Netzteile, Lampendimmer und sogar Leuchtstofflampen.
Für nicht sinusförmige Wellenformen gilt: Der Scheitelfaktor kann erheblich höher sein, was auf höhere Spitzenwerte im Verhältnis zu den Effektivwerten hinweist.
Dies ist wichtig, um die Beanspruchung von Netzteilen und Geräten beurteilen zu können.
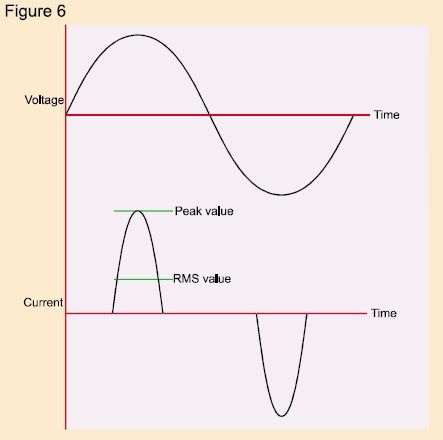
Ein typisches Schaltnetzteil bezieht Strom aus der Wechselstromversorgung, wie in Abb. 6 dargestellt.
Es ist klar, dass der Scheitelfaktor der dargestellten Stromwellenform viel größer als 1,414 ist – tatsächlich haben die meisten Schaltnetzteile und Motordrehzahlregler einen Stromscheitelfaktor von 3 oder mehr.
Daraus folgt, dass ein großer Stromscheitelfaktor eine zusätzliche Belastung für die Geräte darstellt, die eine solche Last versorgen, da die Geräte in der Lage sein müssen, die großen Spitzenströme zu liefern, die mit der verzerrten Wellenform verbunden sind.
Dies ist insbesondere dann relevant, wenn die Last von einer Stromquelle mit begrenzter Impedanz, beispielsweise einem Standby-Wechselrichter, versorgt wird.
Daher ist es klar, dass es bei Wechselstromgeräten wichtig ist, den Scheitelfaktor des aufgenommenen Stroms sowie dessen Effektivstrom zu kennen.
6. Harmonische Verzerrung
Wenn eine Last eine Verzerrung der Stromwellenform verursacht, ist es neben der Kenntnis des Scheitelfaktors hilfreich, den Grad der Verzerrung der Wellenform zu quantifizieren.
Harmonische Verzerrungen treten auf, wenn eine nicht sinusförmige Stromwellenform Frequenzen enthält, die ganzzahlige Vielfache der Grundfrequenz sind. Diese Harmonischen können zu zusätzlichen Verlusten und Belastungen des Stromnetzes führen.
Die Beobachtung mit einem Oszilloskop zeigt die Verzerrung an, jedoch nicht den Grad der Verzerrung.
Durch Fourier-Analyse lässt sich zeigen, dass eine nicht sinusförmige Stromwellenform aus einer Grundkomponente bei der Versorgungsfrequenz und einer Reihe von Harmonischen besteht (d. h. Komponenten bei Frequenzen, die ganzzahlige Vielfache der Versorgungsfrequenz sind).
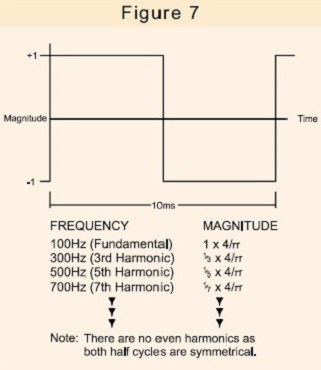
Beispielsweise besteht eine 100-Hz-Rechteckwelle aus den in Abb. 7 gezeigten Komponenten.
Eine Rechteckwelle ist im Vergleich zu einer reinen Sinuswelle deutlich verzerrt. Die Stromwellenform, die beispielsweise von einem Schaltnetzteil, einem Lampendimmer oder sogar einem drehzahlgeregelten Waschmaschinenmotor erzeugt wird, kann jedoch noch bedeutendere Harmonische enthalten.
Abb. 8. Zeigt den von einem gängigen SMPS-Modell aufgenommenen Strom zusammen mit dem Oberwellengehalt dieses Stroms.
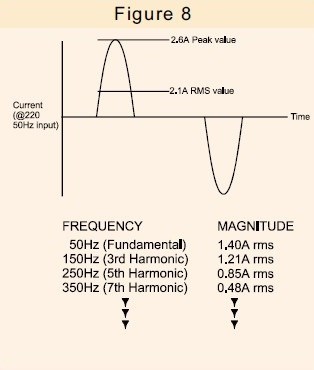
Der einzige Nutzstrom ist die Grundstromkomponente, da nur diese nutzbare Leistung erzeugen kann.
Der zusätzliche Oberschwingungsstrom fließt nicht nur innerhalb des Netzteils selbst, sondern auch in allen mit dem Netzteil verbundenen Verteilungskabeln, Transformatoren und Schaltanlagen und verursacht so zusätzliche Verluste.
Ein hoher Oberwellengehalt kann die Stromqualität und -effizienz beeinträchtigen. Daher wird man sich zunehmend darüber bewusst, dass die von Geräten erzeugten Oberwellen begrenzt werden müssen. In vielen Ländern gibt es Regelungen, die verbindliche Grenzwerte für den für bestimmte Lasttypen zulässigen Oberwellenstrom festlegen.
Solche Regulierungskontrollen finden durch die Verwendung international anerkannter Standards wie IEC555, der bald durch IEC1000-3 ersetzt wird, immer größere Verbreitung.
Daher müssen sich Geräteentwickler stärker darüber im Klaren sein, ob und in welcher Höhe ihre Produkte Oberschwingungen erzeugen.
7. Messung von AC-Parametern
Für Wechselstromanbieter und Gerätehersteller sind die besprochenen Wechselstromparameter von entscheidender Bedeutung. Viele der heute auf dem Markt erhältlichen Messgeräte sind jedoch schwierig zu bedienen oder verfügen nicht über die erforderliche Funktionalität und Genauigkeit, insbesondere bei verzerrten oder verrauschten Eingangssignalen.
Voltech Instruments begegnet diesen Herausforderungen durch die Entwicklung und Herstellung fortschrittlicher Leistungsmessgeräte. Unsere Lösungen decken ein breites Spektrum an Anforderungen ab, von der allgemeinen Leistungsmessung bis hin zu komplexen und anspruchsvollen Leistungsanalyseaufgaben.