Teoría de CA
Las complejas formas de onda de corriente y voltaje asociadas con muchas de las aplicaciones actuales de energía CA plantean problemas de medición específicos.
Un buen punto de partida para abordar algunos de estos problemas es comprender las medidas y términos básicos utilizados, y las relaciones entre ellos.
1. RMS (valor cuadrático medio)
El valor RMS es el medio más utilizado y útil para especificar el valor tanto del voltaje como de la corriente CA. El valor RMS de una forma de onda de CA indica el nivel de potencia disponible en esa forma de onda, siendo este uno de los atributos más importantes de cualquier fuente de CA.
El cálculo de un valor RMS se puede describir mejor considerando una forma de onda de corriente CA y su efecto de calentamiento asociado, como el que se muestra en la figura 1(a) a continuación:
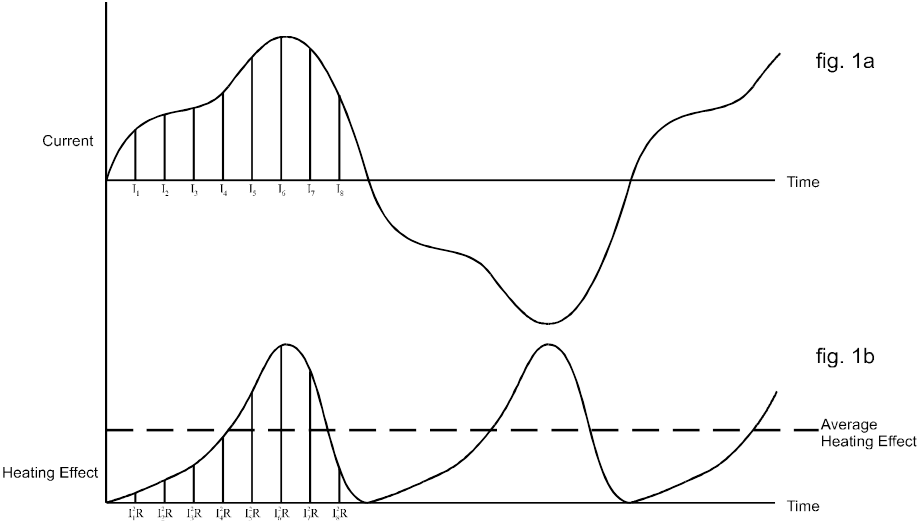
Si se considera que esta corriente fluye a través de una resistencia, el efecto de calentamiento en cualquier instante viene dado por la ecuación:
Al dividir el ciclo actual en coordenadas equiespaciadas, se puede determinar la variación del efecto de calentamiento con el tiempo como se muestra en la fig. 1b.
El efecto de calentamiento promedio (potencia) viene dado por:
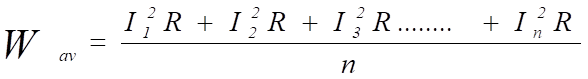
Si quisiéramos encontrar el valor equivalente de corriente que produciría el valor promedio del efecto de calentamiento que se muestra arriba, entonces se aplica lo siguiente:
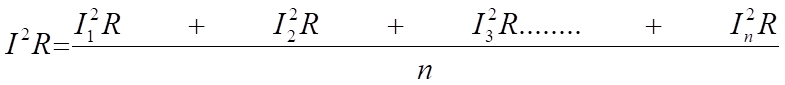
por lo tanto
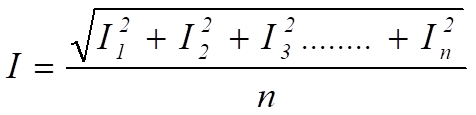
= la raíz cuadrada de la media de los cuadrados de la corriente
= el valor RMS de la corriente .
Este valor a menudo se denomina valor efectivo de la forma de onda de CA, ya que es equivalente a la corriente directa que produce el mismo efecto de calentamiento (potencia) en la carga resistiva.
Vale la pena señalar que para una forma de onda sinusoidal pura que; Valor RMS = valor pico / SQRT(2) = valor pico * 0,707
2. Valor promedio
El valor promedio de una forma de onda como la que se muestra en la fig. 2 está dado por:
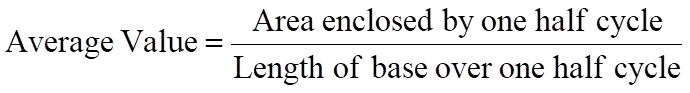
Está claro que el valor promedio sólo puede tener un significado real durante medio ciclo de la forma de onda, ya que para una forma de onda simétrica el valor medio o promedio durante un ciclo completo es cero.
La mayoría de los multímetros simples determinan los valores de CA mediante la rectificación de onda completa de la forma de onda de CA seguida de un cálculo del valor medio.
Sin embargo, dichos medidores se calibrarán en RMS y utilizarán la relación conocida entre RMS y el promedio para una forma de onda sinusoidal.
es decir: RMS = 1,11 x media.
Sin embargo, para formas de onda que no sean una onda sinusoidal pura, las lecturas de dichos medidores no serán válidas.
3. Potencia real y aparente (W y VA)
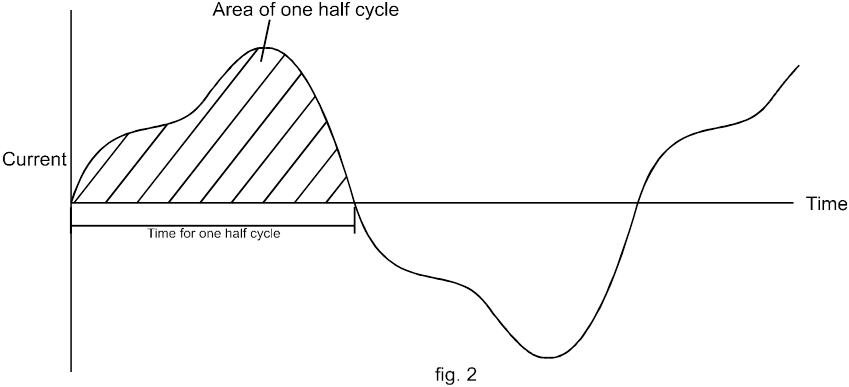
Si una fuente de voltaje sinusoidal de, digamos, 100 V RMS se conecta a una carga resistiva de, digamos, 100 ohmios, entonces el voltaje y la corriente se pueden representar como en la fig. 3a. y se dice que están en fase.
La potencia que fluye desde el suministro a la carga en cualquier instante está dada por el valor del producto del voltaje por la corriente en ese instante, como se ilustra en la fig. 3b.
De esto se puede ver que la potencia que fluye hacia la carga fluctúa (al doble de la frecuencia de suministro) entre 0 y 200 vatios y que la potencia promedio entregada a la carga es igual a 100 vatios, que es lo que se podría esperar de 100 V RMS y una resistencia de 100 ohmios.
Sin embargo, si la carga es reactiva (es decir, contiene inductancia o capacitancia además de resistencia) con una impedancia de 100 ohmios, entonces la corriente que fluye seguirá siendo de 1 A RMS pero ya no estará en fase con el voltaje. Esto se muestra en la figura. 4a. para una carga inductiva con la corriente retrasada en 60 o .
Aunque el flujo de energía continúa fluctuando al doble de la frecuencia del suministro, ahora fluye desde el suministro a la carga durante solo una parte de cada medio ciclo; durante la parte restante, en realidad fluye desde la carga al suministro.
Por lo tanto, el flujo neto promedio hacia la carga es mucho menor que en el caso de una carga resistiva, con solo 50 W de potencia útil entregada a la carga inductiva.
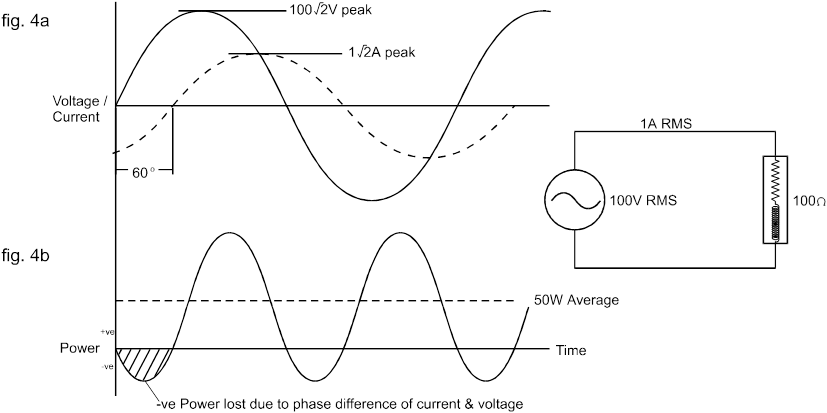
En los dos casos anteriores, el voltaje RMS era igual a 100 V RMS y la corriente era 1 A RMS.
El producto de estos dos valores es la potencia aparente entregada a la carga y se mide en VA de la siguiente manera:
Potencia aparente = Voltios RMS x Amperios RMS
Se ha demostrado que la potencia real entregada depende de la naturaleza de la carga.
No es posible determinar el valor de la potencia real a partir del conocimiento del voltaje y la corriente RMS.
Esto sólo se puede lograr (por ejemplo, para evaluar la pérdida de calor o la eficiencia) mediante el uso de un verdadero medidor de potencia de CA capaz de calcular el producto de los valores instantáneos de voltaje y corriente y mostrar la media del resultado.
4. Factor de potencia
Está claro que, en comparación con los sistemas de CC, la potencia de CA transferida no es simplemente el producto de los valores de tensión y corriente.
También hay que tener en cuenta otro elemento conocido como factor de potencia.
En el ejemplo anterior (potencia real y aparente) con carga inductiva, el factor de potencia es 0,5 porque la potencia útil es exactamente la mitad de la potencia aparente.
Por tanto, podemos definir el factor de potencia como:
En el caso de formas de onda de tensión y corriente sinusoidales, el factor de potencia es en realidad igual al coseno del ángulo de fase entre las formas de onda de tensión y corriente.
Por ejemplo, con la carga inductiva descrita anteriormente, la corriente está retrasada con respecto al voltaje en 60 o , por lo tanto:
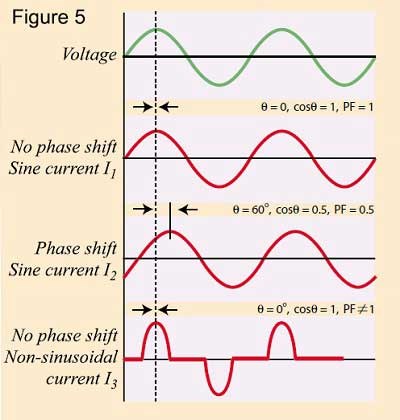
Es por esta razón que a menudo se hace referencia al factor de potencia como cosθ.
Sin embargo, es importante recordar que este es sólo el caso cuando tanto el voltaje como la corriente son sinusoidales (Figura 5, I1 e I2) y que el factor de potencia no es igual a cosθ en ningún otro caso [Figura 5 (I3)].
Esto debe recordarse cuando se utiliza un medidor de factor de potencia que lee cosθ, ya que la lectura no será válida excepto para formas de onda de corriente y tensión sinusoidal pura.
Un verdadero medidor de factor de potencia calculará la relación entre la potencia real y la aparente como se describe anteriormente.
5. Factor de cresta
Ya se ha demostrado que para una forma de onda sinusoidal:
La relación entre pico y RMS se conoce como factor de cresta y se define como:
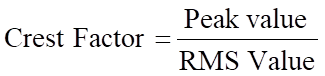
Así, para una sinusoide:
Muchos elementos de los equipos modernos conectados al suministro de CA adoptan formas de onda de corriente no sinusoidales, entre las que se incluyen fuentes de alimentación, atenuadores de lámparas e incluso lámparas fluorescentes.
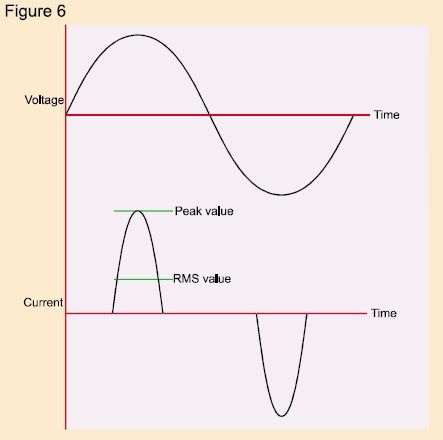
Una fuente de alimentación de modo conmutado típica tomará corriente de la fuente de CA como se muestra en la fig. 6.
Está claro que el factor de cresta de la forma de onda de corriente representada es mucho mayor que 1,414; de hecho, la mayoría de las fuentes de alimentación de modo conmutado y controladores de velocidad de motores tienen un factor de cresta de corriente de 3 o mayor.
Por lo tanto, se deduce que un factor de cresta de corriente grande debe ejercer una presión adicional sobre el equipo que suministra dicha carga, ya que el equipo debe ser capaz de suministrar las grandes corrientes máximas asociadas con la forma de onda distorsionada.
Esto es particularmente relevante si una fuente de energía de impedancia limitada, como un inversor de reserva, suministra la carga.
Por tanto, queda claro que, cuando se trata de equipos de CA, es importante conocer el factor de cresta de la corriente consumida, así como su corriente RMS.
6. Distorsión Armónica
Si una carga introduce distorsión de la forma de onda actual es útil, además de conocer el factor de cresta, cuantificar el nivel de distorsión de la forma de onda.
La observación en un osciloscopio indicará la distorsión pero no el nivel de distorsión.
Mediante el análisis de Fourier se puede demostrar que una forma de onda de corriente no sinusoidal consta de un componente fundamental en la frecuencia de suministro más una serie de armónicos (es decir, componentes en frecuencias que son múltiplos integrales de la frecuencia de suministro).
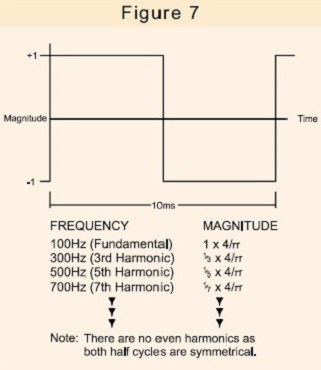
Por ejemplo, una onda cuadrada de 100 Hz consta de los componentes que se muestran en la fig. 7.
Una onda cuadrada está claramente muy distorsionada en comparación con una onda sinusoidal pura. Sin embargo, la forma de onda de corriente generada, por ejemplo, por un SMPS, un atenuador de lámpara o incluso el motor de una lavadora con velocidad controlada, puede contener armónicos de importancia aún mayor.
Fig 8. Muestra la corriente consumida por un modelo SMPS popular junto con el contenido armónico de esa corriente.
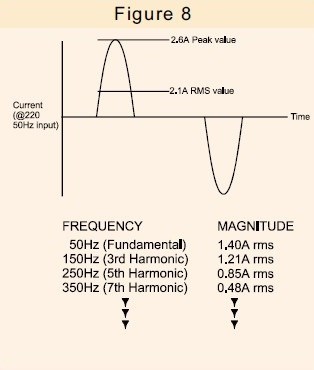
La única corriente útil es el componente fundamental de la corriente, ya que es sólo ésta la que puede generar energía útil.
La corriente armónica adicional no solo fluye dentro de la fuente de alimentación en sí, sino en todos los cables de distribución, transformadores y equipos de conmutación asociados con la fuente de alimentación y, por lo tanto, causará pérdidas adicionales.
Cada vez hay más conciencia de la necesidad de limitar el nivel de armónicos que pueden producir los equipos. En muchos territorios existen controles para proporcionar límites obligatorios sobre el nivel de corriente armónica permitida para ciertos tipos de carga.
Estos controles regulatorios se están generalizando con el uso de estándares reconocidos internacionalmente como IEC555, que pronto será reemplazado por IEC1000-3.
Por lo tanto, es necesario que los diseñadores de equipos sean más conscientes de si sus productos generan armónicos y en qué nivel.
7. Medición de parámetros de CA
Se ha demostrado que los parámetros de CA descritos anteriormente pueden ser importantes tanto para los fabricantes de equipos como para los proveedores de energía de CA. Sin embargo, es común que la instrumentación que se utiliza para estas aplicaciones sea incómoda de usar o incapaz de proporcionar la funcionalidad o precisión requerida, especialmente cuando las señales que se analizan tienen ruido o están distorsionadas.
Voltech Instruments se especializa en el desarrollo y fabricación de instrumentación de medición de potencia diseñada para brindar soluciones para una amplia gama de aplicaciones, desde medición de potencia de uso general hasta las tareas de análisis de potencia más complejas y exigentes.