Théorie du courant alternatif
Dans les applications d'alimentation CA avancées d'aujourd'hui, les améliorations en matière de mesure et de compréhension du courant et de la tension complexes sont devenues plus cruciales.
Ce guide fournit un aperçu des paramètres fondamentaux de la théorie AC et de son importance.
L'apprentissage des concepts de base des valeurs RMS, des valeurs moyennes, de la puissance réelle et apparente, du facteur de puissance, du facteur de crête, de la distorsion harmonique et des techniques de mesure vous permettra de mieux comprendre la théorie fondamentale du courant alternatif.
MIS À JOUR LE 29 AOÛT 2024
1. RMS (valeur quadratique moyenne)
La valeur RMS est le moyen le plus couramment utilisé et le plus utile pour spécifier la valeur de la tension et du courant alternatif.
La valeur RMS d'une forme d'onde CA est celle qui, lorsqu'elle est appliquée à un circuit donné pendant un temps donné, produit la même dépense d'énergie lorsqu'une source CC est appliquée au même circuit pendant le même intervalle de temps.
La valeur RMS est essentielle pour évaluer la puissance disponible à partir d'une source CA et une mesure critique pour quantifier la tension et le courant CA.
CALCUL:
Le calcul d'une valeur RMS peut être mieux décrit en considérant une forme d'onde de courant alternatif et son effet de chauffage associé tel que celui illustré dans la figure 1(a) ci-dessous :
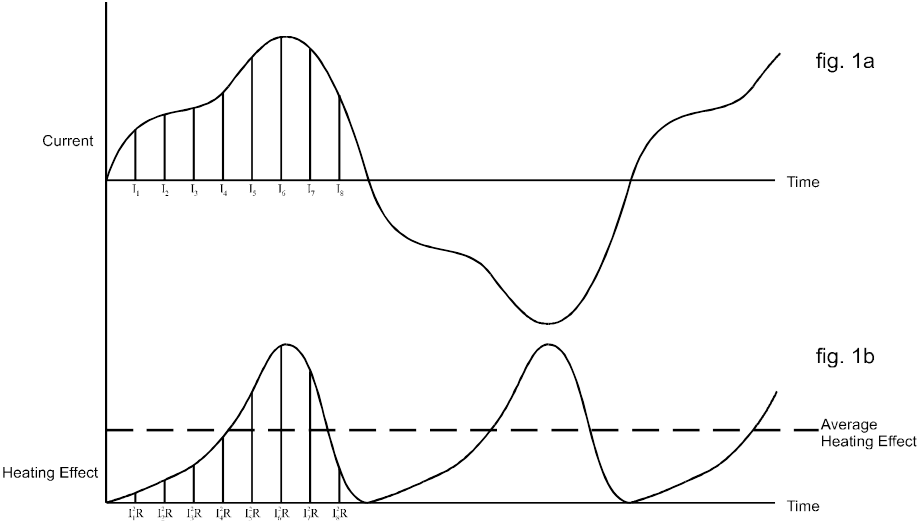
Si l'on considère que ce courant circule à travers une résistance, l'effet de chauffage à tout instant est donné par l'équation :
![]()
En divisant le cycle actuel en coordonnées également espacées, la variation de l'effet de chauffage avec le temps peut être déterminée comme indiqué dans la fig. 1b.
L'effet de chauffage moyen (puissance) est donné par :
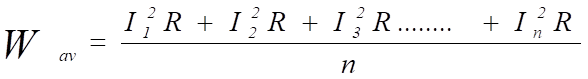
Si nous voulions trouver la valeur équivalente du courant qui produirait la valeur moyenne de l'effet de chauffage indiquée ci-dessus, alors ce qui suit s'applique :
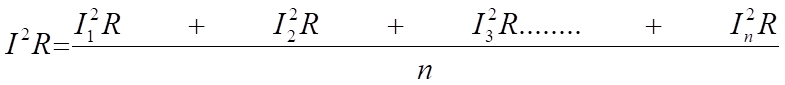
donc
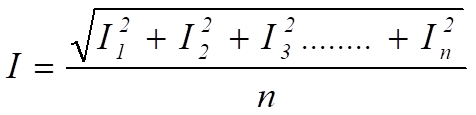
= la racine carrée de la moyenne des carrés du courant
= la valeur RMS du courant .
Cette valeur est souvent appelée valeur effective de la forme d'onde CA car elle est équivalente au courant continu qui produit le même effet de chauffage (puissance) dans la charge résistive.
Pour une forme d’onde sinusoïdale pure :
RMS = Valeur de crête / SQRT (2)
= Valeur maximale x 0,707
2. Valeur moyenne
La valeur moyenne d'une onde sinusoïdale est la moyenne de toutes les valeurs instantanées d'un demi-cycle, car la valeur moyenne sur un cycle complet est nulle pour les formes d'onde symétriques comme la forme d'onde CA.
La valeur moyenne d'une forme d'onde telle que celle représentée sur la figure 2 est donnée par :
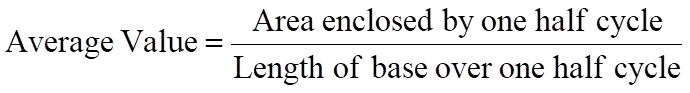
Il est clair que la valeur moyenne ne peut avoir de véritable signification que sur un demi-cycle de la forme d'onde, car pour une forme d'onde symétrique, la valeur moyenne sur un cycle complet est nulle.
La plupart des multimètres simples déterminent les valeurs CA par rectification complète de la forme d'onde CA suivie d'un calcul de la valeur moyenne.
Ces compteurs seront cependant étalonnés en RMS et utiliseront la relation connue entre RMS et moyenne pour une forme d'onde sinusoïdale
c'est-à-dire : RMS = 1,11 x moyenne.
Cependant, pour les formes d'onde autres qu'une onde sinusoïdale pure, les lectures de ces compteurs seront invalides.
3. Puissance réelle et apparente (W et VA)
La puissance réelle est la quantité réelle de puissance utilisée ou dissipée dans un circuit tandis que la puissance apparente est la combinaison de la puissance réelle et de la puissance réactive.
Il s'agit du produit de la tension et du courant d'un circuit sans référence à l'angle de phase.
Étant donné que la puissance apparente a une relation directe avec la valeur RMS (les deux sont définies comme la quantité réelle et la valeur efficace du courant alternatif et de la tension alternative), la formule simple pour la puissance apparente est S (apparente) = V (rms) x I (rms) et est mesurée en Volt-Ampères (VA).
APPLICATION:
Si une source de tension sinusoïdale de 100 V RMS est connectée à une charge résistive de 100 Ohms, la tension et le courant peuvent être représentés comme dans la fig. 3a et sont dits en phase.
La puissance qui circule de l'alimentation à la charge à tout instant est donnée par la valeur du produit de la tension et du courant à cet instant, comme illustré dans la fig. 3b.
On peut en déduire que la puissance circulant dans la charge fluctue (à deux fois la fréquence d'alimentation) entre 0 et 200 watts et que la puissance moyenne délivrée à la charge est égale à 100 watts, ce que l'on pourrait attendre d'une tension de 100 V RMS et d'une résistance de 100 ohms.

Cependant, si la charge est réactive (c'est-à-dire qu'elle contient une inductance ou une capacité ainsi qu'une résistance) avec une impédance de 100 ohms, le courant qui circule sera toujours de 1 A RMS mais ne sera plus en phase avec la tension. Ceci est illustré sur la figure 4a. pour une charge inductive avec un courant en retard de 60 o .
Bien que le flux d'énergie continue de fluctuer à une fréquence deux fois supérieure à celle de l'alimentation, il circule désormais de l'alimentation vers la charge pendant seulement une partie de chaque demi-cycle ; pendant la partie restante, il circule en fait de la charge vers l'alimentation.
Le flux net moyen dans la charge est donc beaucoup plus faible que dans le cas d'une charge résistive, avec seulement 50 W de puissance utile délivrée dans la charge inductive.
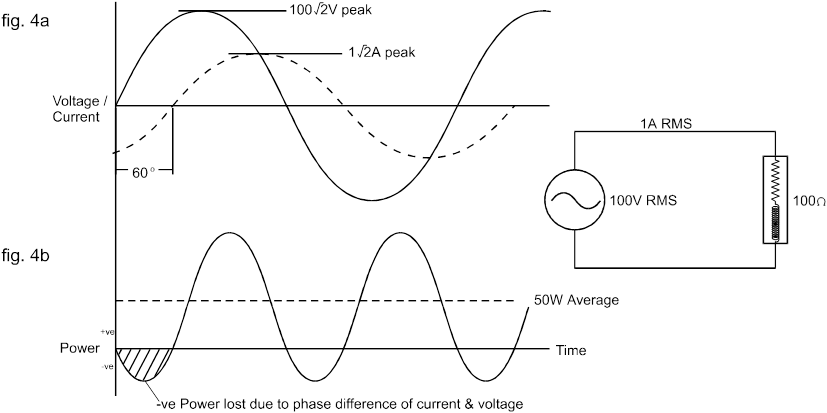
Dans les deux cas ci-dessus, la tension RMS était égale à 100 V RMS et le courant était de 1 A RMS.
Le produit de ces deux valeurs est la puissance apparente délivrée à la charge et est mesurée en VA comme suit :
Puissance apparente = Volts RMS x Ampères RMS
La simple connaissance de la tension et du courant RMS ne suffit pas à déterminer la puissance réelle.
Pour évaluer avec précision la puissance, par exemple pour évaluer la perte de chaleur ou l’efficacité, nous avons besoin d’un véritable wattmètre CA.
Cet appareil calcule le produit des valeurs instantanées de tension et de courant puis affiche la moyenne de ce produit.
4. Facteur de puissance
Il est clair que, par rapport aux systèmes à courant continu, la puissance alternative transférée n'est pas simplement le produit des valeurs de tension et de courant.
Le facteur de puissance est défini comme le rapport entre la puissance réelle et la puissance apparente.

Dans le cas de formes d'onde sinusoïdales pures de courant et de tension alternatifs, le facteur de puissance dépend de la phase de l'angle dans lequel il est mesuré.
Le facteur de puissance sera égal à l'unité (1) lorsque la tension et le courant sont dans la même phase. (et Cos (0) = 1)
Le facteur de puissance en retard se produit lorsque le courant est en retard sur la tension d'un angle aigu.
Le facteur de puissance avancé se produit lorsque le courant devance la tension d'un angle aigu.
Le facteur de puissance sera nul lorsque la tension et le courant sont déphasés d'exactement 90 degrés. - cela signifie que la puissance RÉELLE est également nulle.
Importance : Le facteur de puissance affecte l’efficacité énergétique et la gestion de la charge dans les systèmes CA.
CALCUL:
Dans l'exemple précédent (puissance réelle et apparente) avec une charge inductive, le facteur de puissance est de 0,5 car la puissance utile est exactement la moitié de la puissance apparente.
Dans le cas de formes d'onde de tension et de courant sinusoïdales, le facteur de puissance est en fait égal au cosinus de l'angle de phase entre les formes d'onde de tension et de courant.
Par exemple, avec la charge inductive décrite précédemment, le courant est en retard de 60 o sur la tension, donc :
![]()
C'est pour cette raison que le facteur de puissance est souvent appelé cosθ.
Il est cependant important de se rappeler que cela n'est le cas que lorsque la tension et le courant sont tous deux sinusoïdaux (Figure 5, I1 et I2) et que le facteur de puissance n'est pas égal à cosθ dans les autres cas [Figure 5 (I3)].
Il faut s'en souvenir lors de l'utilisation d'un wattmètre qui lit cosθ, car la lecture ne sera valide que pour les formes d'onde de tension et de courant sinusoïdales pures.
Un véritable wattmètre calculera le rapport entre la puissance réelle et la puissance apparente comme décrit ci-dessus.
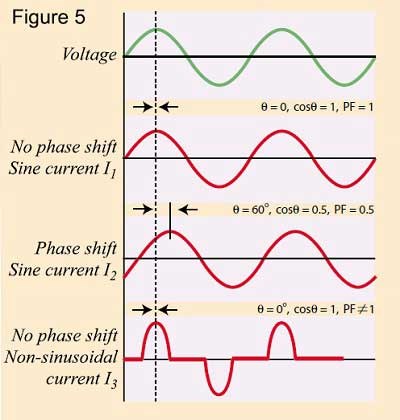
5. Facteur de crête
Il a déjà été démontré que pour une forme d’onde sinusoïdale :
![]()
La relation entre la valeur de crête et la valeur efficace (RMS) est connue sous le nom de facteur de crête et est définie comme le rapport entre la valeur de crête et la valeur efficace (RMS).
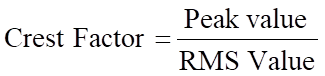
Ainsi pour une sinusoïde :
![]()
De nombreux équipements modernes connectés à l'alimentation secteur prennent des formes d'onde de courant non sinusoïdales, notamment les alimentations électriques, les variateurs de lumière et même les lampes fluorescentes.
Pour les formes d'onde non sinusoïdales : le facteur de crête peut être significativement plus élevé, indiquant des valeurs de crête plus élevées par rapport aux valeurs RMS.
Ceci est important pour évaluer la contrainte exercée sur les alimentations et les équipements.
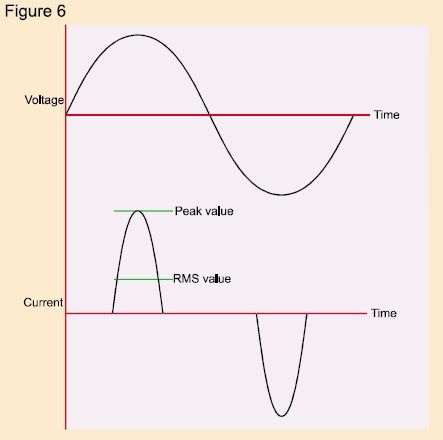
Une alimentation à découpage typique prend le courant de l'alimentation CA comme indiqué dans la fig. 6.
Il est clair que le facteur de crête de la forme d'onde de courant représentée est bien supérieur à 1,414 – en effet, la plupart des alimentations à découpage et des contrôleurs de vitesse de moteur ont un facteur de crête de courant de 3 ou plus.
Il s'ensuit donc qu'un facteur de crête de courant élevé doit exercer une contrainte supplémentaire sur l'équipement fournissant une telle charge, car l'équipement doit être capable de fournir les courants de crête élevés associés à la forme d'onde déformée.
Ceci est particulièrement pertinent lorsqu'une source d'alimentation à impédance limitée, telle qu'un onduleur de secours, alimente la charge.
Il est donc clair que, lorsqu'un équipement CA est impliqué, il est important de connaître le facteur de crête du courant consommé ainsi que son courant RMS.
6. Distorsion harmonique
Si une charge introduit une distorsion de la forme d'onde du courant, il est utile, en plus de connaître le facteur de crête, de quantifier le niveau de distorsion de la forme d'onde.
La distorsion harmonique se produit lorsqu'une forme d'onde de courant non sinusoïdale contient des fréquences qui sont des multiples entiers de la fréquence fondamentale. Ces harmoniques peuvent entraîner des pertes et des contraintes supplémentaires sur le système électrique.
L'observation sur un oscilloscope indiquera la distorsion mais pas le niveau de distorsion.
L'analyse de Fourier permet de démontrer qu'une forme d'onde de courant non sinusoïdale se compose d'une composante fondamentale à la fréquence d'alimentation plus une série d'harmoniques (c'est-à-dire des composantes à des fréquences qui sont des multiples entiers de la fréquence d'alimentation).
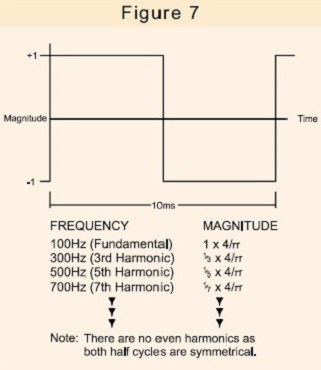
Par exemple, une onde carrée de 100 Hz est constituée des composants représentés sur la figure 7.
Une onde carrée est clairement très déformée par rapport à une onde sinusoïdale pure. Cependant, la forme d'onde du courant consommé par un SMPS, un variateur de lumière ou même un moteur de machine à laver à vitesse variable peut contenir des harmoniques encore plus importantes.
La figure 8 montre le courant consommé par un modèle SMPS populaire ainsi que le contenu harmonique de ce courant.
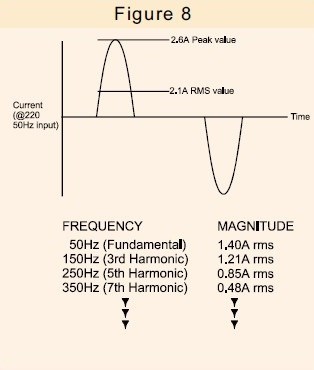
Le seul courant utile est la composante fondamentale du courant, car c'est elle seule qui peut générer une puissance utile.
Le courant harmonique supplémentaire circule non seulement dans l'alimentation électrique elle-même, mais également dans tous les câbles de distribution, transformateurs et appareillages de commutation associés à l'alimentation électrique et entraînera ainsi des pertes supplémentaires.
Un contenu harmonique élevé peut affecter la qualité et l'efficacité de l'énergie et il existe une prise de conscience croissante de la nécessité de limiter le niveau d'harmoniques que les équipements peuvent produire. Des contrôles existent dans de nombreux territoires pour fixer des limites obligatoires sur le niveau de courant harmonique autorisé pour certains types de charge.
Ces contrôles réglementaires se généralisent avec l’utilisation de normes reconnues internationalement telles que la norme IEC555, bientôt remplacée par la norme IEC1000-3.
Il est donc nécessaire que les concepteurs d’équipements soient davantage sensibilisés à la question de savoir si leurs produits génèrent des harmoniques et à quel niveau.
7. Mesure des paramètres AC
Pour les fournisseurs d'énergie CA et les fabricants d'équipements, les paramètres CA évoqués sont essentiels. Mais de nombreux instruments de mesure actuellement sur le marché peuvent être difficiles à utiliser ou manquer de fonctionnalités et de précision, en particulier lorsqu'ils fonctionnent avec des entrées déformées ou bruyantes.
Voltech Instruments répond à ces défis en développant et en fabriquant des instruments de mesure de puissance avancés. Nos solutions répondent à un large éventail de besoins, allant de la mesure de puissance à usage général aux tâches d'analyse de puissance complexes et très exigeantes.