Teoria AC
Nelle applicazioni avanzate di alimentazione CA odierne, i miglioramenti nella misurazione e nella comprensione di correnti e tensioni complesse sono diventati ancora più cruciali.
Questa guida fornisce una panoramica dei parametri fondamentali della teoria della corrente alternata e della sua importanza.
Imparare i concetti di base dei valori RMS, dei valori medi, della potenza reale e apparente, del fattore di potenza, del fattore di cresta, della distorsione armonica e delle tecniche di misurazione ti consentirà di comprendere meglio la teoria fondamentale della corrente alternata.
AGGIORNATO 29 AGOSTO 2024
1. RMS (valore quadratico medio)
Il valore RMS è il mezzo più comunemente utilizzato e utile per specificare il valore sia della tensione che della corrente alternata.
Il valore RMS di un'onda CA è il valore che, applicato a un dato circuito per un dato periodo di tempo, produce lo stesso dispendio di energia quando una sorgente CC viene applicata allo stesso circuito per lo stesso intervallo di tempo.
Il valore RMS è essenziale per valutare la potenza disponibile da una sorgente CA e una misura critica per quantificare la tensione e la corrente CA.
CALCOLO:
Il calcolo di un valore RMS può essere descritto al meglio considerando una forma d'onda di corrente alternata e il suo effetto di riscaldamento associato, come mostrato nella figura 1(a) sottostante:
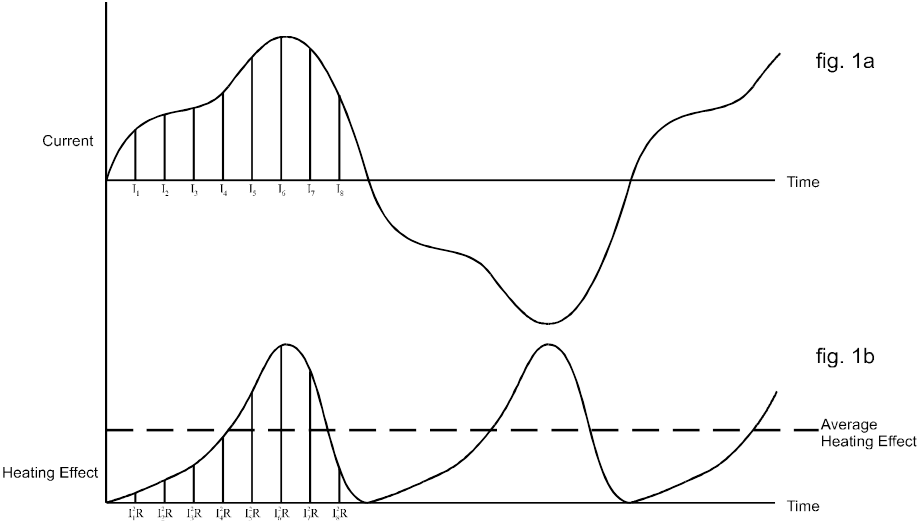
Se si considera che questa corrente fluisce attraverso una resistenza, l'effetto di riscaldamento in ogni istante è dato dall'equazione:
![]()
Dividendo il ciclo corrente in coordinate equidistanti è possibile determinare la variazione dell'effetto riscaldante nel tempo, come mostrato nella figura 1b.
L'effetto riscaldante medio (potenza) è dato da:
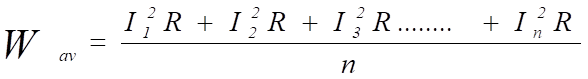
Se volessimo trovare il valore equivalente della corrente che produrrebbe il valore medio dell'effetto riscaldante mostrato sopra, allora si applica quanto segue:
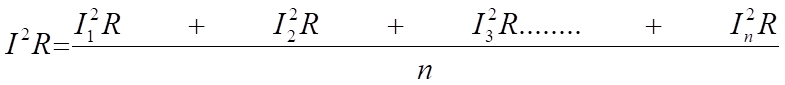
Perciò
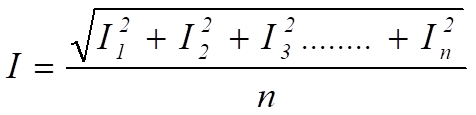
= la radice quadrata della media dei quadrati della corrente
= il valore RMS della corrente .
Questo valore è spesso definito valore effettivo della forma d'onda CA in quanto equivale alla corrente continua che produce lo stesso effetto riscaldante (potenza) nel carico resistivo.
Per una forma d'onda sinusoidale pura:
RMS = Valore di picco / SQRT (2)
= Valore di picco x 0,707
2. Valore medio
Il valore medio di un'onda sinusoidale è la media di tutti i valori istantanei di mezzo ciclo, poiché il valore medio su un ciclo completo è zero per forme d'onda simmetriche come la forma d'onda CA.
Il valore medio di una forma d'onda come quella mostrata nella fig. 2 è dato da:
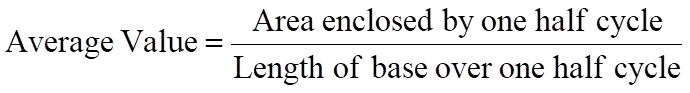
È chiaro che il valore medio può avere un significato reale solo su metà ciclo della forma d'onda, poiché per una forma d'onda simmetrica il valore medio su un ciclo completo è zero.
La maggior parte dei multimetri più semplici determina i valori CA mediante la rettificazione a onda intera della forma d'onda CA seguita dal calcolo del valore medio.
Tali misuratori saranno tuttavia calibrati in RMS e utilizzeranno la nota relazione tra RMS e media per una forma d'onda sinusoidale
ovvero: RMS = 1,11 x media.
Tuttavia, per forme d'onda diverse dall'onda sinusoidale pura, le letture di tali misuratori non saranno valide.
3. Potenza reale e apparente (W e VA)
La potenza reale è la quantità effettiva di potenza utilizzata o dissipata in un circuito, mentre la potenza apparente è la combinazione di potenza reale e potenza reattiva.
È il prodotto della tensione e della corrente di un circuito, senza riferimento all'angolo di fase.
Poiché la potenza apparente ha una relazione diretta con il valore RMS (entrambi sono stati definiti come la quantità effettiva e il valore effettivo della corrente alternata e della tensione alternata), la formula semplice per la potenza apparente è S (apparente) = V(rms) x I (rms) e si misura in Volt-Ampere (VA).
APPLICAZIONE:
Se una sorgente di tensione sinusoidale di, diciamo, 100 V RMS è collegata a un carico resistivo di, diciamo, 100 Ohm, allora la tensione e la corrente possono essere rappresentate come nella figura 3a. e si dice che sono in fase.
La potenza che fluisce dall'alimentazione al carico in ogni istante è data dal valore del prodotto della tensione per la corrente in quell'istante, come illustrato nella fig. 3b.
Da ciò si può vedere che la potenza che fluisce nel carico fluttua (a una frequenza doppia rispetto a quella di alimentazione) tra 0 e 200 Watt e che la potenza media erogata al carico è pari a 100 Watt, ovvero quanto ci si potrebbe aspettare da 100 V RMS e una resistenza di 100 Ohm.

Tuttavia, se il carico è reattivo (ovvero contiene induttanza o capacità oltre a resistenza) con un'impedenza di 100 ohm, la corrente che scorre sarà ancora 1 A RMS ma non sarà più in fase con la tensione. Ciò è mostrato nella fig. 4a. per un carico induttivo con la corrente in ritardo di 60 o .
Sebbene il flusso di potenza continui a fluttuare a una frequenza doppia rispetto a quella di alimentazione, esso fluisce dall'alimentazione al carico solo durante una parte di ogni semiciclo; nella parte rimanente fluisce effettivamente dal carico all'alimentazione.
Il flusso netto medio nel carico è quindi molto più piccolo rispetto al caso di un carico resistivo, con solo 50 W di potenza utile erogata al carico induttivo.
In entrambi i casi sopra menzionati la tensione RMS era pari a 100 V RMS e la corrente era pari a 1 A RMS.
Il prodotto di questi due valori è la potenza apparente erogata al carico e si misura in VA come segue:
Potenza apparente = Volt RMS x Ampere RMS
La semplice conoscenza della tensione e della corrente RMS non è sufficiente per determinare la potenza effettiva.
Per valutare con precisione la potenza, ad esempio per valutare la perdita di calore o l'efficienza, abbiamo bisogno di un vero misuratore di potenza CA.
Questo dispositivo calcola il prodotto dei valori istantanei di tensione e corrente e quindi visualizza la media di questo prodotto.
4. Fattore di potenza
È chiaro che, rispetto ai sistemi a corrente continua, la potenza alternata trasferita non è semplicemente il prodotto dei valori di tensione e corrente.
Il fattore di potenza è definito come il rapporto tra potenza reale e potenza apparente.

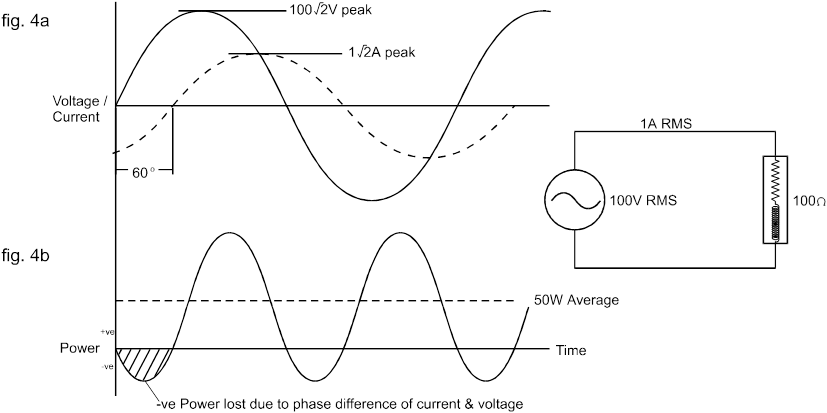
Nel caso di forme d'onda sinusoidali pure di corrente alternata e tensione, il fattore di potenza dipende dalla fase dell'angolo in cui viene misurato.
Il fattore di potenza sarà unitario (1) dove tensione e corrente sono nella stessa fase. (e Cos (0) = 1)
Il fattore di potenza ritardato si verifica quando la corrente è in ritardo rispetto alla tensione di un angolo acuto.
Il fattore di potenza anticipatore si verifica quando la corrente anticipa la tensione di un angolo acuto.
Il fattore di potenza sarà zero quando la tensione e la corrente sono sfasate esattamente di 90 gradi. Ciò significa che anche la potenza REALE è zero.
Importanza: il fattore di potenza influisce sull'efficienza energetica e sulla gestione del carico nei sistemi di aria condizionata.
CALCOLO:
Nell'esempio precedente (potenza reale e apparente) con un carico induttivo, il fattore di potenza è 0,5 perché la potenza utile è esattamente la metà della potenza apparente.
Nel caso di forme d'onda sinusoidali di tensione e corrente, il fattore di potenza è in realtà uguale al coseno dell'angolo di fase tra le forme d'onda di tensione e corrente.
Ad esempio, con il carico induttivo descritto in precedenza, la corrente è in ritardo rispetto alla tensione di 60 o , quindi:
![]()
Per questo motivo il fattore di potenza viene spesso indicato con cosθ.
È tuttavia importante ricordare che questo è il caso solo quando sia la tensione che la corrente sono sinusoidali (Figura 5, I1 e I2) e che il fattore di potenza non è uguale a cosθ in nessun altro caso [Figura 5 (I3)].
Questo è importante da tenere presente quando si utilizza un misuratore del fattore di potenza che legge cosθ, poiché la lettura non sarà valida se non per forme d'onda di tensione e corrente puramente sinusoidali.
Un vero misuratore del fattore di potenza calcolerà il rapporto tra potenza reale e apparente come descritto sopra.
5. Fattore di cresta
È già stato dimostrato che per una forma d'onda sinusoidale:
![]()
Il rapporto tra valore di picco e valore efficace è noto come fattore di cresta ed è definito come il rapporto tra valore di picco e valore efficace (RMS).
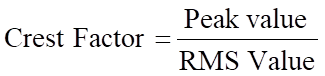
Quindi per una sinusoide:
![]()
Molti dispositivi moderni collegati all'alimentazione in corrente alternata assumono forme d'onda di corrente non sinusoidali; tra questi rientrano gli alimentatori, i dimmer per lampade e persino le lampade fluorescenti.
Per forme d'onda non sinusoidali: il fattore di cresta può essere significativamente più alto, indicando valori di picco maggiori rispetto ai valori RMS.
Ciò è importante per valutare lo stress sugli alimentatori e sulle apparecchiature.
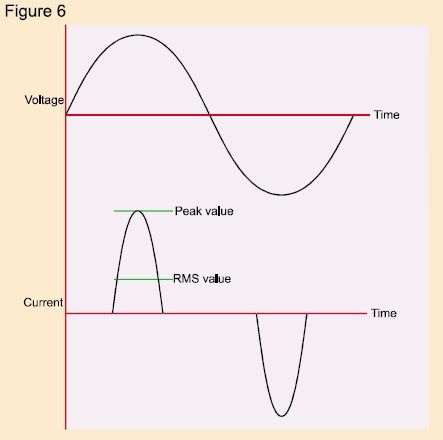
Un tipico alimentatore switching preleva la corrente dalla rete elettrica come mostrato nella figura 6.
È chiaro che il fattore di cresta della forma d'onda di corrente rappresentata è molto maggiore di 1,414: in effetti, la maggior parte degli alimentatori switching e dei regolatori di velocità dei motori hanno un fattore di cresta di corrente pari o superiore a 3.
Ne consegue che un elevato fattore di cresta di corrente deve sottoporre a sollecitazione aggiuntiva l'apparecchiatura che alimenta tale carico, poiché l'apparecchiatura deve essere in grado di fornire le elevate correnti di picco associate alla forma d'onda distorta.
Ciò è particolarmente rilevante quando il carico è alimentato da una fonte di alimentazione a impedenza limitata, come un inverter di standby.
È quindi chiaro che, quando si tratta di apparecchiature a corrente alternata, è importante conoscere il fattore di cresta della corrente assorbita nonché la sua corrente RMS.
6. Distorsione armonica
Se un carico introduce una distorsione della forma d'onda della corrente è utile, oltre a conoscere il fattore di cresta, quantificare il livello di distorsione della forma d'onda.
La distorsione armonica si verifica quando una forma d'onda di corrente non sinusoidale contiene frequenze che sono multipli interi della frequenza fondamentale. Queste armoniche possono causare perdite e stress aggiuntivi sul sistema di alimentazione.
L'osservazione tramite oscilloscopio indicherà la distorsione ma non il suo livello.
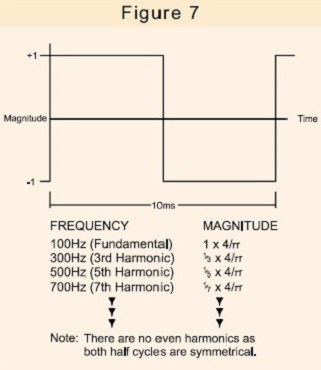
Mediante l'analisi di Fourier è possibile dimostrare che un'onda di corrente non sinusoidale è composta da una componente fondamentale alla frequenza di alimentazione più una serie di armoniche (ovvero componenti a frequenze che sono multipli interi della frequenza di alimentazione).
Ad esempio, un'onda quadra da 100 Hz è composta dai componenti mostrati nella figura 7.
Un'onda quadra è chiaramente molto distorta rispetto a un'onda sinusoidale pura. Tuttavia, la forma d'onda di corrente disegnata ad esempio da un SMPS, un dimmer per lampade o persino un motore di lavatrice a velocità controllata può contenere armoniche di importanza ancora maggiore.
La figura 8 mostra la corrente assorbita da un modello SMPS diffuso insieme al contenuto armonico di tale corrente.
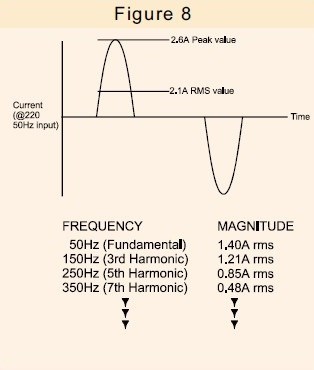
L'unica corrente utile è la componente fondamentale della corrente, poiché è l'unica che può generare energia utile.
La corrente armonica aggiuntiva non scorre solo all'interno dell'alimentatore stesso, ma anche in tutti i cavi di distribuzione, nei trasformatori e nelle apparecchiature di commutazione associati all'alimentatore, causando quindi ulteriori perdite.
Un elevato contenuto armonico può influire sulla qualità e l'efficienza dell'energia e c'è una crescente consapevolezza della necessità di limitare il livello di armoniche che le apparecchiature possono produrre. In molti territori esistono controlli per fornire limiti obbligatori sul livello di corrente armonica consentita per determinati tipi di carico.
Tali controlli normativi stanno diventando sempre più diffusi con l'uso di standard riconosciuti a livello internazionale, come IEC555, che sarà presto sostituito da IEC1000-3.
È quindi necessario che i progettisti di apparecchiature siano maggiormente consapevoli se i loro prodotti generano armoniche e a quale livello.
7. Misurazione dei parametri AC
Per i fornitori di energia CA e i produttori di apparecchiature, i parametri CA discussi sono essenziali. Ma molti degli strumenti di misurazione sul mercato oggi possono essere difficili da usare o non avere funzionalità e accuratezza sufficienti, specialmente quando si lavora con input distorti o rumorosi.
Voltech Instruments affronta queste sfide sviluppando e producendo strumentazione avanzata per la misurazione della potenza. Le nostre soluzioni soddisfano un ampio spettro di esigenze, che vanno dalla misurazione della potenza generica alle attività di analisi della potenza complesse e ad alta richiesta.