Teoria prądu przemiennego
W dzisiejszych zaawansowanych zastosowaniach zasilania prądem przemiennym coraz ważniejsze stają się udoskonalenia w zakresie pomiarów i zrozumienia złożonych zjawisk prądu i napięcia.
W tym przewodniku przedstawiono przegląd podstawowych parametrów teorii prądu przemiennego i ich znaczenie.
Poznanie podstawowych pojęć wartości RMS, wartości średnich, mocy czynnej i pozornej, współczynnika mocy, współczynnika szczytu, zniekształceń harmonicznych i technik pomiarowych pozwoli Ci lepiej zrozumieć podstawową teorię prądu przemiennego.
AKTUALIZACJA 29 SIERPNIA 2024
1. RMS (wartość średnia kwadratowa)
Wartość RMS jest najczęściej używanym i najprzydatniejszym sposobem określania wartości napięcia i prądu przemiennego.
Wartość skuteczna prądu przemiennego to wartość, która przyłożona do danego obwodu przez dany czas powoduje taki sam wydatek energii, jak przyłożona do tego samego obwodu przez ten sam przedział czasu wartość skuteczna prądu stałego.
Wartość RMS jest istotna przy ocenie mocy dostępnej ze źródła prądu przemiennego oraz stanowi kluczowy pomiar napięcia i prądu przemiennego.
OBLICZENIE:
Obliczenie wartości RMS można najlepiej opisać, biorąc pod uwagę kształt fali prądu przemiennego i związany z nim wpływ na nagrzewanie, jak pokazano na rys. 1(a) poniżej:
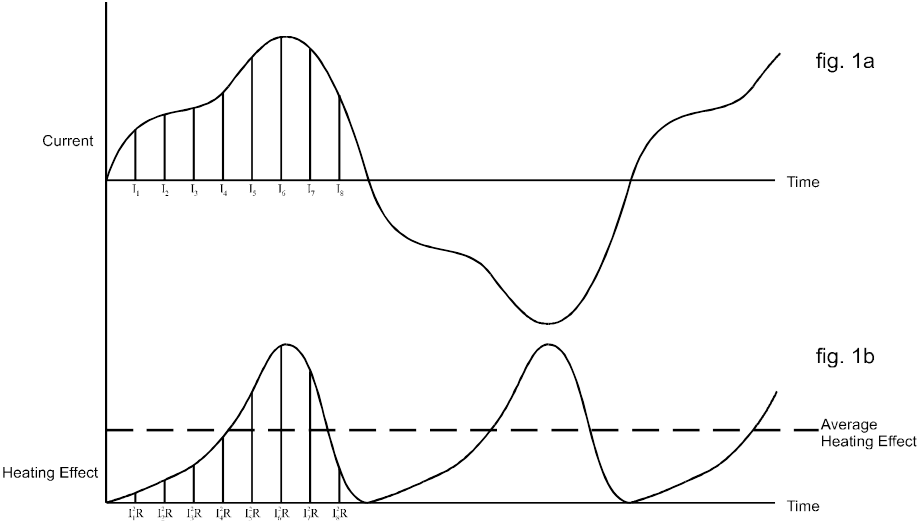
Jeżeli przyjmiemy, że prąd ten przepływa przez rezystancję, efekt cieplny w dowolnej chwili jest podany równaniem:
![]()
Dzieląc cykl prądu na współrzędne o równych odstępach, można określić zmianę efektu grzewczego w czasie, jak pokazano na rys. 1b.
Średni efekt grzewczy (moc) podawany jest wzorem:
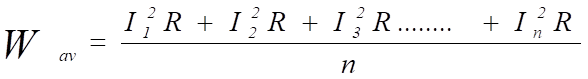
Gdybyśmy chcieli znaleźć wartość prądu równoważną, która wytworzyłaby średnią wartość efektu cieplnego przedstawioną powyżej, wówczas stosuje się następujące równanie:
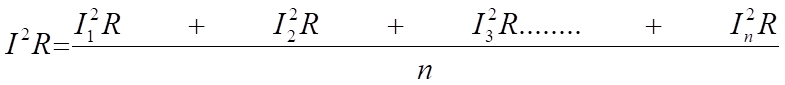
W związku z tym
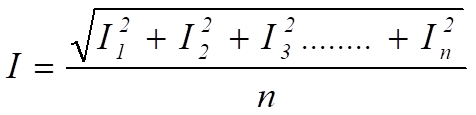
= pierwiastek kwadratowy średniej kwadratów prądu
= wartość skuteczna prądu .
Wartość tę często nazywa się wartością skuteczną przebiegu prądu przemiennego, ponieważ odpowiada ona prądowi stałemu, który wytwarza taki sam efekt cieplny (moc) w obciążeniu rezystancyjnym.
Dla czystej sinusoidalnej formy fali:
RMS = wartość szczytowa / pierwiastek kwadratowy (2)
= Wartość szczytowa x 0,707
2. Wartość średnia
Wartość średnia fali sinusoidalnej to średnia wszystkich chwilowych wartości jednej drugiej fazy, ponieważ w przypadku przebiegów symetrycznych, takich jak przebieg prądu przemiennego, wartość średnia w całym cyklu wynosi zero.
Średnia wartość przebiegu takiego jak pokazany na rys. 2 jest podana wzorem:
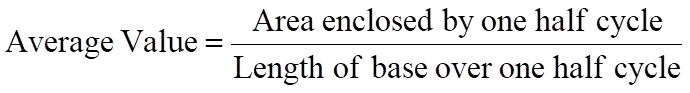
Oczywiste jest, że wartość średnia może mieć rzeczywiste znaczenie tylko w ciągu jednej połowy cyklu przebiegu, ponieważ w przypadku przebiegu symetrycznego wartość średnia w całym cyklu wynosi zero.
Większość prostych multimetrów określa wartości prądu przemiennego poprzez prostowanie pełnookresowe przebiegu prądu przemiennego, a następnie obliczenie wartości średniej.
Jednakże takie mierniki będą kalibrowane w wartościach RMS i będą wykorzystywać znaną zależność między wartością RMS a wartością średnią dla przebiegu sinusoidalnego
tj.: RMS = 1,11 x średnia.
Jednakże w przypadku przebiegów innych niż czysta fala sinusoidalna odczyty takich mierników będą nieprawidłowe.
3. Moc rzeczywista i pozorna (W i VA)
Moc czynna to faktyczna ilość mocy wykorzystywanej lub rozpraszanej w obwodzie, natomiast moc pozorna to kombinacja mocy czynnej i mocy biernej.
Jest to iloczyn napięcia i prądu w obwodzie bez odniesienia do kąta fazowego.
Ponieważ moc pozorna ma bezpośredni związek z wartością skuteczną (obie zostały zdefiniowane jako rzeczywista ilość i wartość skuteczna prądu przemiennego i napięcia przemiennego), prosty wzór na moc pozorną to S (pozorna) = V(rms) x I (rms) i jest mierzona w woltoamperach (VA).
APLIKACJA:
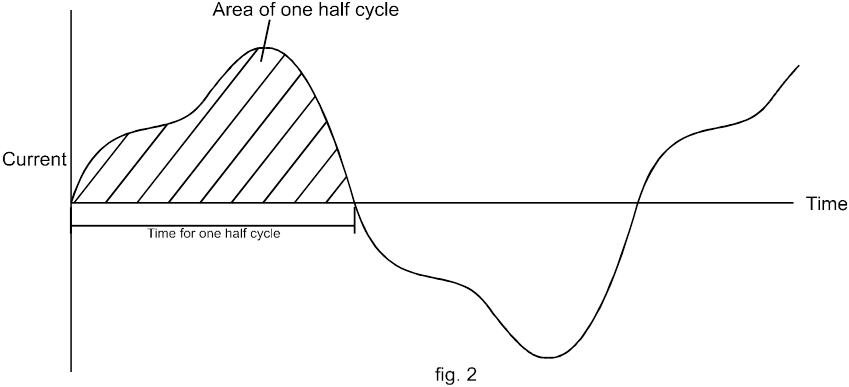
Jeżeli źródło napięcia sinusoidalnego, np. o wartości skutecznej 100 V, zostanie podłączone do obciążenia rezystancyjnego, np. o wartości 100 omów, wówczas napięcie i prąd można przedstawić tak, jak na rys. 3a. Mówi się, że są w fazie.
Moc płynąca ze źródła zasilania do obciążenia w dowolnej chwili jest dana wartością iloczynu napięcia i prądu w tej chwili, jak pokazano na rys. 3b.
Z tego wynika, że moc przepływająca do obciążenia waha się (przy dwukrotności częstotliwości zasilania) w zakresie od 0 do 200 watów, a średnia moc dostarczona do obciążenia wynosi 100 watów – czego można by oczekiwać od napięcia skutecznego 100 V i rezystancji 100 omów.

Jednakże, jeśli obciążenie jest reaktywne (tj. zawiera indukcyjność lub pojemność, a także rezystancję) z impedancją 100 omów, wówczas prąd, który płynie, będzie nadal wynosił 1 A RMS, ale nie będzie już w fazie z napięciem. Jest to pokazane na rys. 4a. dla obciążenia indukcyjnego z prądem opóźnionym o 60 o .
Mimo że przepływ mocy nadal waha się z częstotliwością dwukrotnie większą od częstotliwości zasilania, teraz płynie ona z zasilania do obciążenia tylko przez część każdego półcyklu – podczas pozostałej części płynie faktycznie od obciążenia do zasilania.
W związku z tym średni przepływ netto do obciążenia jest znacznie mniejszy niż w przypadku obciążenia rezystancyjnego, gdyż do obciążenia indukcyjnego dostarczane jest jedynie 50 W mocy użytecznej.
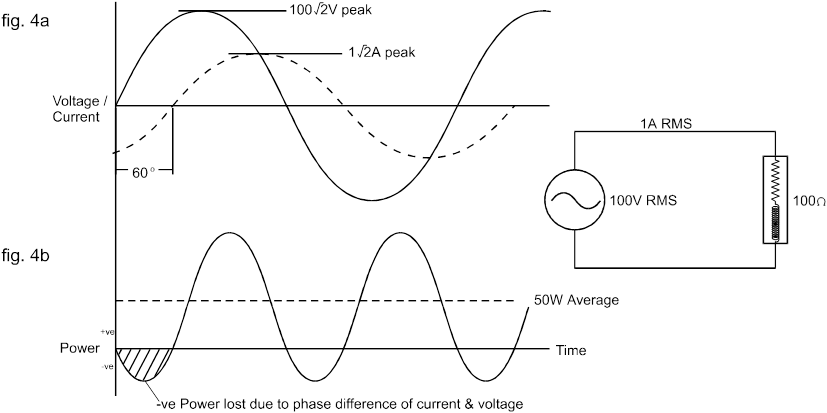
W obu powyższych przypadkach napięcie skuteczne wynosiło 100 V RMS, a natężenie prądu wynosiło 1 A RMS.
Iloczyn tych dwóch wartości to moc pozorna dostarczona do obciążenia i jest mierzona w VA w następujący sposób:
Moc pozorna = Wolty RMS x Ampery RMS
Sama znajomość wartości skutecznej napięcia i natężenia prądu nie jest wystarczająca do określenia rzeczywistej mocy.
Aby dokładnie ocenić zużycie energii — na przykład w celu oszacowania strat ciepła lub wydajności — potrzebujemy prawdziwego miernika energii prądu przemiennego.
Urządzenie to oblicza iloczyn chwilowych wartości napięcia i natężenia prądu, a następnie wyświetla średnią wartość tego iloczynu.
4. Współczynnik mocy
Oczywiste jest, że w porównaniu z systemami prądu stałego, przesyłana moc prądu przemiennego nie jest po prostu iloczynem wartości napięcia i prądu.
Współczynnik mocy definiuje się jako stosunek mocy czynnej do mocy pozornej.

W przypadku czystych przebiegów sinusoidalnych prądu i napięcia przemiennego współczynnik mocy zależy od fazy kąta, w którym jest mierzony.
Współczynnik mocy będzie równy jedności (1), gdy napięcie i prąd będą w tej samej fazie. (i cosinus (0) = 1)
Współczynnik mocy opóźniony ma miejsce, gdy prąd opóźnia się względem napięcia pod ostrym kątem.
Współczynnik mocy wyprzedzający to taki, w którym prąd wyprzedza napięcie o ostry kąt.
Współczynnik mocy będzie równy zero, gdy napięcie i prąd będą przesunięte w fazie o dokładnie 90 stopni. Oznacza to, że RZECZYWISTA moc również będzie równa zero.
Znaczenie: Współczynnik mocy ma wpływ na efektywność energetyczną i obsługę obciążeń w systemach prądu przemiennego.
OBLICZENIE:
W poprzednim przykładzie (moc czynna i pozorna) z obciążeniem indukcyjnym współczynnik mocy wynosi 0,5, ponieważ moc użyteczna stanowi dokładnie połowę mocy pozornej.
W przypadku sinusoidalnych przebiegów napięcia i prądu współczynnik mocy jest w rzeczywistości równy cosinusowi kąta fazowego między przebiegami napięcia i prądu.
Na przykład przy obciążeniu indukcyjnym opisanym wcześniej, prąd opóźnia się w stosunku do napięcia o 60o , zatem:
![]()
Z tego powodu współczynnik mocy jest często określany jako cosθ.
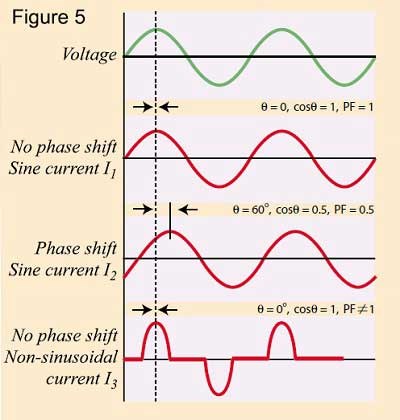
Należy jednak pamiętać, że dotyczy to jedynie sytuacji, gdy napięcie i prąd mają kształt sinusoidalny (rysunek 5, I1 i I2) oraz że współczynnik mocy nie jest równy cosθ w żadnym innym przypadku [rysunek 5 (I3)].
Należy o tym pamiętać, korzystając z miernika współczynnika mocy odczytującego cosθ, gdyż odczyt będzie wiarygodny tylko dla czystych sinusoidalnych przebiegów napięcia i prądu.
Miernik rzeczywistego współczynnika mocy oblicza stosunek mocy czynnej do mocy pozornej, jak opisano powyżej.
5. Współczynnik szczytu
Wykazano już, że dla przebiegu sinusoidalnego:
![]()
Zależność między wartością szczytową a wartością skuteczną (RMS) nazywana jest współczynnikiem szczytu i definiowana jest jako stosunek wartości szczytowej do wartości skutecznej (RMS).
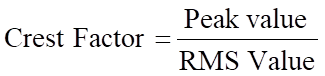
Tak więc dla sinusoidy:
![]()
Wiele nowoczesnych urządzeń podłączonych do zasilania prądem zmiennym przyjmuje niesinusoidalne kształty przebiegów prądu. Należą do nich zasilacze, ściemniacze lamp, a nawet lampy fluorescencyjne.
W przypadku przebiegów niesinusoidalnych: współczynnik szczytu może być znacznie wyższy, co wskazuje na większe wartości szczytowe w porównaniu do wartości RMS.
Jest to istotne dla oceny obciążenia zasilaczy i sprzętu.
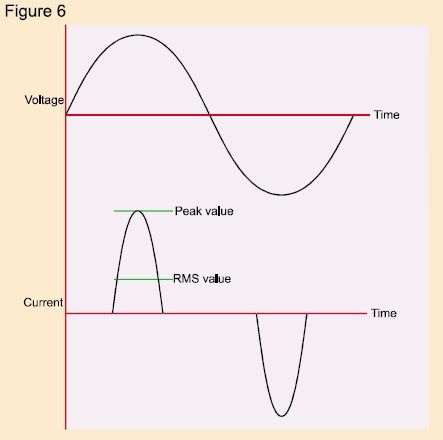
Typowy zasilacz impulsowy pobiera prąd z zasilacza prądu przemiennego, jak pokazano na rys. 6.
Wyraźnie widać, że współczynnik szczytu przedstawionego przebiegu prądu jest znacznie większy niż 1,414 – w istocie większość zasilaczy impulsowych i regulatorów prędkości obrotowej silnika ma współczynnik szczytu prądu wynoszący 3 lub więcej.
Z tego wynika, że duży współczynnik szczytu prądu musi dodatkowo obciążać urządzenia zasilające takie obciążenie, ponieważ urządzenia te muszą być zdolne do dostarczania dużych prądów szczytowych związanych ze zniekształconym przebiegiem.
Jest to szczególnie istotne w przypadku, gdy obciążenie jest zasilane ze źródła zasilania o ograniczonej impedancji, takiego jak inwerter zapasowy.
Zatem jest oczywiste, że w przypadku urządzeń prądu przemiennego istotna jest znajomość współczynnika szczytu pobieranego prądu, jak również jego wartości skutecznej prądu.
6. Zniekształcenia harmoniczne
Jeżeli obciążenie wprowadza zniekształcenie przebiegu prądu, przydatne jest, oprócz znajomości współczynnika szczytu, określenie poziomu zniekształcenia kształtu przebiegu.
Zniekształcenie harmoniczne występuje, gdy niesinusoidalny przebieg prądu zawiera częstotliwości, które są całkowitymi wielokrotnościami częstotliwości podstawowej. Te harmoniczne mogą prowadzić do dodatkowych strat i obciążeń systemu elektroenergetycznego.
Obserwacja oscyloskopu pozwoli wykryć zniekształcenia, ale nie ich poziom.
Za pomocą analizy Fouriera można wykazać, że przebieg prądu niesinusoidalnego składa się ze składowej podstawowej o częstotliwości zasilania i szeregu harmonicznych (czyli składowych o częstotliwościach będących całkowitymi wielokrotnościami częstotliwości zasilania).
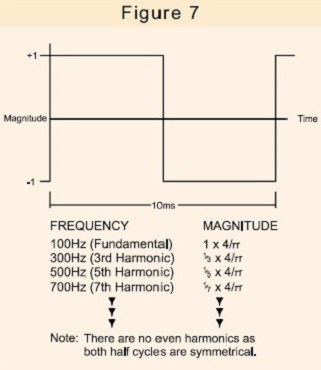
Na przykład fala prostokątna o częstotliwości 100 Hz składa się ze składowych pokazanych na rys. 7.
Fala prostokątna jest wyraźnie bardzo zniekształcona w porównaniu do czystej fali sinusoidalnej. Jednak kształt fali prądu generowany na przykład przez SMPS, ściemniacz lampy lub nawet silnik pralki z regulacją prędkości może zawierać harmoniczne o jeszcze większym znaczeniu.
Rys. 8. Przedstawia prąd pobierany przez popularny model SMPS wraz z zawartością harmonicznych tego prądu.
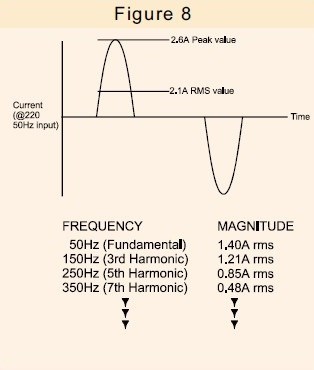
Jedynym użytecznym prądem jest podstawowy składnik prądu, gdyż tylko on może generować użyteczną moc.
Dodatkowy prąd harmoniczny płynie nie tylko w samym zasilaczu, ale także we wszystkich kablach dystrybucyjnych, transformatorach i rozdzielnicach podłączonych do zasilacza, powodując w ten sposób dodatkowe straty.
Wysoka zawartość harmonicznych może wpływać na jakość i wydajność zasilania, a coraz większa jest świadomość konieczności ograniczenia poziomu harmonicznych, jakie sprzęt może wytwarzać. W wielu obszarach istnieją kontrole zapewniające obowiązkowe limity poziomu prądu harmonicznego dozwolonego dla niektórych typów obciążeń.
Tego rodzaju kontrole regulacyjne stają się coraz powszechniejsze dzięki stosowaniu uznawanych na całym świecie norm, takich jak IEC555, która wkrótce zostanie zastąpiona normą IEC1000-3.
Istnieje zatem potrzeba zwiększenia świadomości projektantów sprzętu co do tego, czy ich produkty generują harmoniczne i na jakim poziomie.
7. Pomiar parametrów prądu przemiennego
Dla dostawców prądu przemiennego i producentów sprzętu omawiane parametry prądu przemiennego są niezbędne. Jednak wiele dostępnych obecnie na rynku przyrządów pomiarowych może być trudnych w obsłudze lub nie mieć wystarczającej funkcjonalności i dokładności, zwłaszcza podczas pracy ze zniekształconymi lub zaszumionymi sygnałami wejściowymi.
Voltech Instruments stawia czoła tym wyzwaniom, opracowując i produkując zaawansowane urządzenia do pomiaru mocy. Nasze rozwiązania zaspokajają szerokie spektrum potrzeb, od ogólnego pomiaru mocy po złożone i wymagające zadania analizy mocy.