Los conceptos básicos de los transformadores
Este documento explica la teoría básica y el funcionamiento de los transformadores.
ACTUALIZADO EL 29 DE AGOSTO DE 2024
1. Introducción a los transformadores
Los transformadores son componentes esenciales de los sistemas eléctricos y electrónicos.
Proporcionan aislamiento eléctrico y realizan la importante tarea de transformar voltajes y corrientes. Si bien el proceso de diseño a veces puede considerarse un “arte”, su construcción y funcionalidad se basan en principios fundamentales de la física.
Este artículo profundiza en los conceptos básicos de la teoría, el funcionamiento y el rendimiento de los transformadores, ofreciendo información sobre sus características principales y consideraciones prácticas.
2. Teoría básica del transformador
Los transformadores proporcionan aislamiento eléctrico entre circuitos, lo que es crucial para la seguridad y la funcionalidad en diferentes aplicaciones.
Un transformador consta de un núcleo magnético con bobinas primarias y secundarias enrolladas a su alrededor.
Cuando se aplica un voltaje alterno a la bobina primaria, se generará una corriente alterna que corresponde al flujo magnético alterno en el núcleo.
Este flujo induce un voltaje tanto en la bobina primaria como en la secundaria; por lo tanto: la Ley de inducción de Faraday en acción.
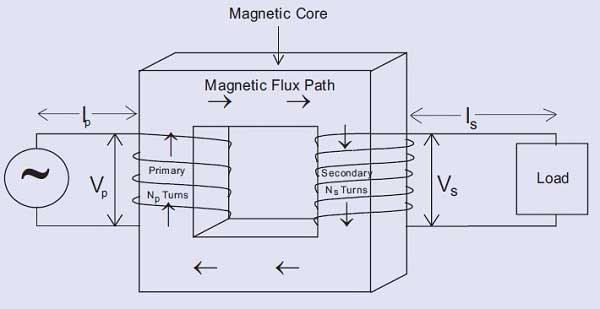
La figura anterior representa los elementos esenciales de un transformador: un núcleo magnético con una bobina primaria y secundaria enrolladas en las extremidades del núcleo magnético.
Un voltaje alterno (Vp) aplicado al primario crea una corriente alterna (Ip) a través del primario.
Esta corriente produce un flujo magnético alterno en el núcleo magnético.
Este flujo magnético alterno induce un voltaje en cada vuelta del primario y en cada vuelta del secundario.
Como el flujo es constante, es decir, el mismo tanto en el primario como en el secundario:
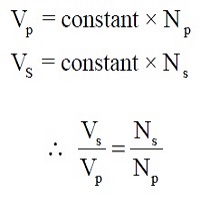
Esta ecuación muestra que se puede utilizar un transformador para aumentar o reducir un voltaje de CA controlando la relación entre las espiras primarias y secundarias. (Acción del transformador de voltaje).
También se puede demostrar que:
Voltiamperios primarios = Voltiamperios secundarios
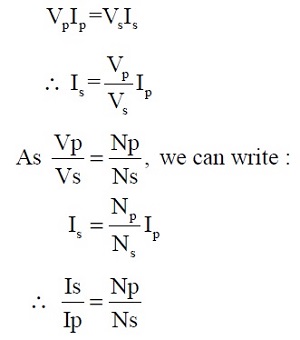
Esta ecuación muestra que se puede utilizar un transformador para aumentar o reducir una corriente alterna controlando la relación entre las espiras primarias y secundarias.
(Acción del transformador de corriente)
Se observará que no hay conexión eléctrica entre los devanados primario y secundario.
Por lo tanto, un transformador proporciona un medio para aislar un circuito eléctrico de otro.
Estas características (transformación de voltaje/corriente y aislamiento) no se pueden obtener de manera eficiente por ningún otro medio, con el resultado de que se utilizan transformadores en casi todos los equipos eléctricos y electrónicos del mundo.
3. Curvas BH
Las propiedades magnéticas del material del núcleo influyen en gran medida en el rendimiento de un transformador. Cuando se activa la bobina primaria del transformador, la corriente magnetizante crea una fuerza magnetizante (H), que genera un flujo magnético (B) en el núcleo. Esta relación entre B y H está representada por la curva BH del material.
La fuerza de magnetización (H) es igual al producto de la corriente de magnetización por el número de vueltas, y se expresa en amperios - vueltas.
Las curvas BH ilustran la densidad de flujo como función de la fuerza de magnetización, lo que significa que a medida que (H) aumenta, (B) aumenta hasta que el material del núcleo se satura.
En la saturación, aumentos adicionales de (H) no aumentan significativamente (B) y esa es la razón por la cual diseñar transformadores para que funcionen por debajo del punto de saturación es crucial para garantizar un rendimiento eficiente.
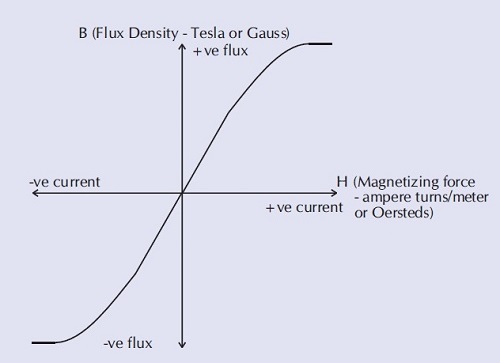
De la curva BH se puede ver que, a medida que la fuerza de magnetización aumenta desde cero, el flujo aumenta hasta un cierto valor máximo de flujo.
Por encima de este nivel, si se incrementa aún más la fuerza de magnetización, no se produce un aumento significativo del flujo. Se dice que el material magnético está "saturado".
Un transformador normalmente está diseñado para garantizar que la densidad de flujo magnético esté por debajo del nivel que causaría saturación.
La densidad de flujo se puede determinar utilizando la siguiente ecuación:
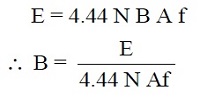
Dónde:
E representa el valor RMS del voltaje aplicado.
N representa el número de vueltas del devanado.
B representa el valor máximo de la densidad de flujo magnético en el núcleo (Tesla).
A representa el área de la sección transversal del material magnético en el núcleo (metros cuadrados).
f representa la frecuencia de los voltios aplicados.
Nota
1 Tesla = 1 Weber/metro²
1 Weber/m² = 10.000 Gauss
1 amperio-vuelta por metro = 4 px 10-3 Oersteds
En la práctica, todos los materiales magnéticos, una vez magnetizados, conservan parte de su magnetización incluso cuando la fuerza de magnetización se reduce a cero.
Este efecto se conoce como "remanencia" y da como resultado que la curva BH del material muestre una respuesta a una fuerza de magnetización decreciente que es diferente a la respuesta a una fuerza de magnetización creciente.
En la práctica, los materiales magnéticos reales tienen una curva BH como la siguiente:
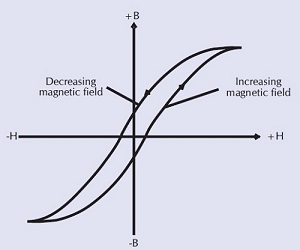
La curva que se muestra arriba se denomina bucle de "histéresis" del material y representa la respuesta BH real del material. (La primera curva BH representa el promedio o la media de la respuesta del bucle BH real).
La pendiente de la curva BH, el nivel de saturación y el tamaño del bucle de histéresis dependen del tipo de material utilizado y de otros factores.
Esto se ilustra con los siguientes ejemplos:
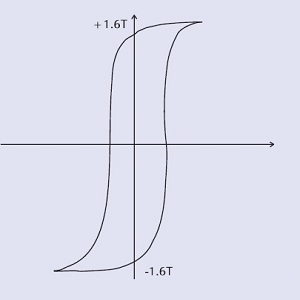 | Núcleo de hierro de baja calidad Densidad de flujo de alta saturación Bucle grande = gran pérdida de histéresis Adecuado para 50/60 Hz |
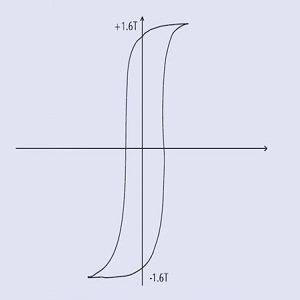 | Núcleo de hierro de alto grado Densidad de flujo de alta saturación Bucle medio = pérdida de histéresis media Adecuado para transformadores de 400 Hz. |
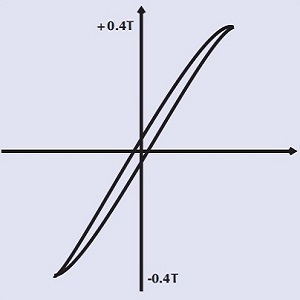 | Núcleo de ferrita: sin espacio de aire Densidad de flujo de saturación media Bucle pequeño = pequeña pérdida de histéresis Adecuado para transformadores de alta frecuencia. |
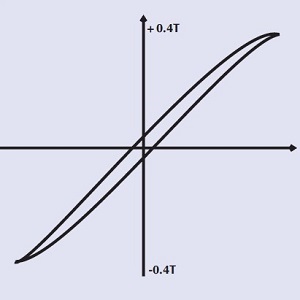 | Núcleo de ferrita: gran espacio de aire Bucle pequeño = pequeña pérdida de histéresis Adecuado para inductores de alta frecuencia con gran corriente CC. |
4. Pérdida por histéresis
La curva BH exhibe un fenómeno llamado histéresis.
Se trata de un fenómeno en el que la magnetización del material del núcleo va por detrás de la fuerza de magnetización; las pérdidas de energía resultantes de este evento se conocen como pérdida por histéresis.
Los materiales con bucles de histéresis más grandes incurren en mayores pérdidas.
Esta pérdida está representada por el área encerrada dentro del bucle de histéresis BH.
Por lo tanto, los núcleos de los transformadores están diseñados con materiales que tienen baja pérdida de histéresis para mejorar la eficiencia.
5. Pérdida por corrientes de Foucault
Las corrientes de Foucault (también llamadas corrientes de Foucault) son bucles de corriente eléctrica inducidos dentro del material del núcleo por el flujo magnético alterno.
Las corrientes crean una pérdida resistiva que conduce al calentamiento del núcleo, conocido como pérdida por corrientes de Foucault, ya que parecen remolinos o torbellinos.
Para minimizar las pérdidas, los núcleos de los transformadores están hechos de láminas laminadas o materiales de ferrita, que restringen los caminos de estas corrientes.
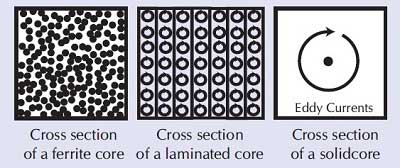
6. Circuito equivalente del transformador
Un transformador ideal con un devanado primario y dos devanados secundarios se puede representar como se muestra a continuación.
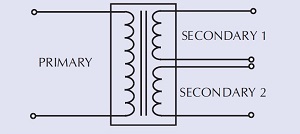
Un transformador de este tipo tiene las siguientes características:
- Sin pérdidas
- Acoplamiento perfecto entre todos los devanados.
- Impedancia de circuito abierto infinita (es decir, no hay corriente de entrada cuando los secundarios están en circuito abierto).
- Aislamiento infinito entre devanados
En la práctica, los transformadores difieren del modelo ideal debido a varias características no ideales. Los circuitos equivalentes de transformadores incorporan estos aspectos:
- Resistencias de bobinado
- Capacitancias
- Pérdidas de núcleo
- Inductancia magnetizante
- Inductancias de fuga
Estas variables ayudan a pronosticar el rendimiento del transformador y las desviaciones del modelo ideal.
Muchas de estas características se pueden representar mediante un circuito equivalente de transformador:
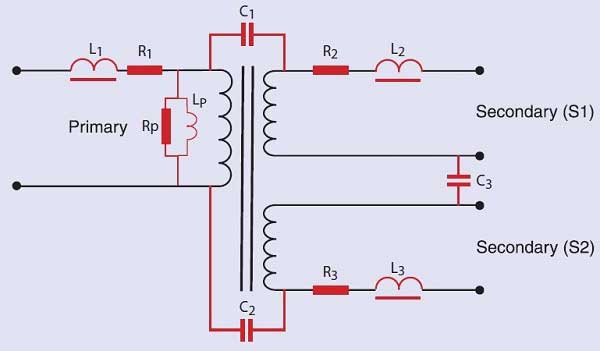
Dónde:
R1, R2, R3 representan la resistencia del cable de bobinado.
C1, C2, C3 representan la capacitancia entre los devanados.
Rp representa las pérdidas que se deben a las pérdidas por corrientes de Foucault y por histéresis. Estas son las pérdidas de potencia reales, a veces llamadas pérdidas de núcleo, que se pueden medir realizando una medición de potencia en circuito abierto. Debido a que no hay corriente de carga, hay muy poca pérdida de cobre I 2 R en el devanado energizado, y los vatios medidos sin carga se deben casi en su totalidad al núcleo.
Lp representa la impedancia debida a la corriente magnetizante. Esta es la corriente que genera la fuerza magnetizante, H, utilizada en los diagramas de bucle BH. Tenga en cuenta que esta corriente puede no ser una onda sinusoidal simple, sino que puede tener una forma distorsionada y puntiaguda, si el transformador se opera en la región no lineal de la curva BH. Este suele ser el caso de los transformadores de tipo laminado de frecuencia de línea.
L1, L2, L3 representan la inductancia de fuga de cada uno de los devanados. (Esto se analiza en detalle en la nota 104-105 de Voltech, "Inductancia de fuga").
7. Conclusiones
El circuito equivalente de un transformador refleja las propiedades reales del circuito magnético que comprende el núcleo y los devanados.
Por lo tanto, el circuito equivalente se puede utilizar con confianza para comprender y predecir el rendimiento eléctrico del transformador en una variedad de situaciones.
Comprender los principios básicos y las consideraciones prácticas del funcionamiento de los transformadores capacita a los ingenieros para diseñar, probar y aplicar transformadores de manera eficaz en diversas aplicaciones.
8. Lectura adicional
Comprender el circuito equivalente de un transformador permite a los ingenieros analizar y predecir su rendimiento eléctrico en diversas condiciones operativas. También ayuda a optimizar los procesos de diseño y prueba, lo que garantiza que los transformadores cumplan con los estándares de calidad y eficiencia.
Otras notas técnicas de esta serie analizan cómo se utilizan los parámetros del circuito equivalente para derivar pruebas prácticas de transformadores para garantizar su calidad en un entorno de fabricación.